THC Science

File:Perspective isometrique cube gris 2.svg

An isometric drawing of a cube. Note that the perimeter of the 2D drawing is a perfect regular hexagon, all the black lines are of equal length and all the cube's faces are the same area.

Isometric projection is a form of graphical projection — more specifically, an axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them is 120°. Isometric projection is one of the projections used in drafting engineering drawings.

The term isometric comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (this is not true of some other forms of graphical projection).

Visualization

Isometric projection dictates the direction of viewing in that the angles between the projection of the x, y, and z axes are all the same, or 120°. For objects with surfaces that are substantially perpendicular to and/or parallel with one another, it corresponds to rotation of the object or camera by +/- 45° about the vertical axis, followed by a rotation of approximately +/- 35.264° [= arcsin(tan(30°))] about the horizontal axis, starting from an orthographic projection relative to an object's face (a perpendicular view to a face of an object).

Isometric projection can be visualized by considering the view of a cubical room from an upper corner, looking towards the opposite lower corner. The x-axis is diagonally down and right, the y-axis is diagonally down and left, and the z-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another.

Mathematical

There are 8 different orientations to obtain an isometric view, depending into which octant the viewer looks. The isometric transform from a point $a_{x,y,z}$ in 3D space to a point $b_{x,y}$ in 2D space looking into the first octant can be written mathematically with rotation matrices as:

{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&{\cos \alpha }&{\sin \alpha }\\0&{-\sin \alpha }&{\cos \alpha }\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta }&0&{-\sin \beta }\\0&1&0\\{\sin \beta }&0&{\cos \beta }\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}={\frac {1}{\sqrt {6}}}{\begin{bmatrix}{\sqrt {3}}&0&-{\sqrt {3}}\\1&2&1\\{\sqrt {2}}&-{\sqrt {2}}&{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}

where $\alpha =\arcsin(\tan(30^{\circ }))\approx 35.264^{\circ }$ and $\beta =45^{\circ }$ . As explained above, this is a rotation around the vertical (here y) axis by $\beta$ , followed by a rotation around the horizontal (here x) axis by $\alpha$ . This is then followed by an orthographic projection to the x-y plane:

{\begin{bmatrix}\mathbf {b} _{x}\\\mathbf {b} _{y}\\0\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}.

The other seven possibilities are obtained by either rotating to the opposite sides or not, and then inverting the view direction or not.^[1]

Limits of isometric projection

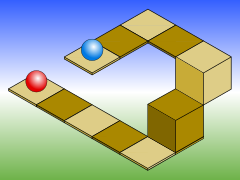
As with all types of parallel projection, objects drawn with isometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for architectural drawings and sprite-based video games, this results in a perceived distortion, as unlike perspective projection, it is not how our eyes or photography work. It also can easily result in situations where depth and altitude are impossible to gauge, as is shown in the illustration to the right. Most contemporary video games have avoided this situation by dropping isometric projection in favor of perspective 3D rendering utilizing vanishing points. Some of the famous "impossible architecture" works of M. C. Escher exploit this isometric limitation. Waterfall (1961) is a good example, in which the building is isometric but the faded background is not.

"Isometric" projection in video games and pixel art

A television set drawn in near- isometric pixel art. Note the 2:1 pixel pattern ratio in this zoomed-in image.

In the fields of computer and video games and pixel art, axonometric projection has been popular because of the ease with which 2D sprites and tile-based graphics can be made to represent a 3D gaming environment. Because objects don't change size as they move about the game field, there is no need for the computer to scale sprites or do the calculations necessary to simulate visual perspective. This allowed older 8-bit and 16-bit game systems (and, more recently, handheld systems) to portray large 3D areas easily. While the depth confusion problems illustrated above can sometimes be a problem, good game design can alleviate this. With the advent of more powerful graphics systems, axonometric projection is becoming less common.

Blurring of the definition

The projection used in videogames usually deviates slightly from "true" isometric due to the limitations of raster graphics. Lines in the x and y axes would not follow a neat pixel pattern if drawn in the required 30° to the horizontal. While modern computers can eliminate this problem using anti-aliasing, earlier computer graphics did not support enough colors or possess enough CPU power to accomplish this. So instead, a 2:1 pixel pattern ratio would be used to draw the x and y axes lines, resulting in these axes following a 26.565° (arctan 0.5) angle to the horizontal. (Game systems that do not use square pixels could, however, yield different angles, including true isometric.) It should therefore be noted that this form of projection is more accurately described as a variation of dimetric projection, since only two of the three angles between the axes are equal (116.565°, 116.565°, 126.87°). Many in video game and pixel art communities, however, continue to mistakenly refer to this projection—as well as other forms of axonometric projection—as "isometric perspective"; the terms "3/4 perspective" and "2.5D" are also commonly used.

More blurring

Increasingly, the term is being applied to games that don't use any form of axonometric projection.^{[citation needed]} Games that use oblique projection^[2]^[3], as well as games that use perspective projection^[4]^[5], are sometimes referred to as being isometric, or "pseudo-isometric", due to visual similarities or similarities in how the game allows a greater field of view over a large playing field. In the case of games that use perspective projection, "bird's-eye view" might be a more appropriate term.

Notable examples of "isometric" computer and video games

File:Liftoff2.png

A game which uses "isometric" graphics (Lincity).

Q*bert (1982) : An arcade hit.
Zaxxon (1982) : Early arcade space flight fight.
Ant Attack (1983) : Home computer game.
Congo Bongo (1983) : Arcade game.
Knight Lore (1984) : Action-adventure computer game.
Marble Madness (1984) : Arcade game.
Spindizzy (1986) : Exploration-based puzzle and maze game for 8-bit computers.
Head over Heels (1987) : Popular action-adventure game from the end of the 8-bit computer era.
La Abadía del Crimen (The Abbey of Crime) (1988).
Populous (1989) : God simulator.
Snake Rattle 'n' Roll (1990) : An action/platformer game.
Cadaver (1990) : Adventure/role-playing game.
Landstalker (1992) : Platformer/role-playing game.
UFO: Enemy Unknown (1993) : A resource management and tactical combat sim.
SimCity 2000 (1993) : City building simulation game.
Little Big Adventure (1994) : an action-adventure game
Transport Tycoon (1994) and its successor, Transport Tycoon Deluxe (1995) : Both are transportation business simulations.
Civilization II (1996) : Turn-based strategy game.
Super Mario RPG (1996) : A role-playing game.
Age of Empires (1997) : History-based RTS game.
Final Fantasy Tactics (1997) : A strategic role-playing game.
Baldur's Gate (1998) : Computer role-playing game in the Forgotten Realms D&D campaign setting.
StarCraft (1998) : Science-fiction real-time strategy game.
The Sims (2000) : A simulation of people controlled by the player.
Diablo II (2000) : A fantasy action Role-playing computer game.

References

^ Ingrid Carlbom, Joseph Paciorek (Dec. 1978), Planar Geometric Projections and Viewing Transformations, vol. v.10 n.4, ACM Computing Surveys (CSUR), pp. p.465-502, doi:10.1145/356744.356750 {{citation}}: |pages= has extra text (help); Check date values in: |date= (help)
^ "GDC 2004: The History of Zelda" (HTML). IGN. March 25, 2004. Retrieved 2007-12-17.
^ Greely, Dave (August 19, 1997). "Has Origin Created the First True Online Game World?" (HTML). Gamasutra. Retrieved 2007-12-17. {{cite web}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
^ "Age of Decadence" (HTML). Iron Tower Studios. Retrieved 2007-07-10.
^ O'Hagan, Steve (August 7, 2003). "PC Review: Silent Storm" (HTML). ComputerAndVideoGames.com. Retrieved 2007-12-13.

External links

[1] Ingrid Carlbom, Joseph Paciorek (Dec. 1978), Planar Geometric Projections and Viewing Transformations, vol. v.10 n.4, ACM Computing Surveys (CSUR), pp. p.465-502, doi:10.1145/356744.356750 {{citation}}: |pages= has extra text (help); Check date values in: |date= (help)

[zelda_gdc-2] "GDC 2004: The History of Zelda" (HTML). IGN. March 25, 2004. Retrieved 2007-12-17.

[gamasutra_uol-3] Greely, Dave (August 19, 1997). "Has Origin Created the First True Online Game World?" (HTML). Gamasutra. Retrieved 2007-12-17. {{cite web}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

[aod_hp-4] "Age of Decadence" (HTML). Iron Tower Studios. Retrieved 2007-07-10.

[cvg_ss-5] O'Hagan, Steve (August 7, 2003). "PC Review: Silent Storm" (HTML). ComputerAndVideoGames.com. Retrieved 2007-12-13.

[1]

[2]

[3]

[4]

[5]

@@ Line 89: / Line 89: @@
 ===More blurring===
-Increasingly, the term is being applied to games that don't use any form of axonometric projection. Games that use [[oblique projection]]<ref name=zelda_gdc>{{cite web | title =GDC 2004: The History of Zelda | publisher =[[IGN]] | date =March 25, 2004 | url =http://cube.ign.com/articles/501/501970p1.html | format =HTML | accessdate =2007-12-17  }}</ref>, as well as games that use [[perspective projection]]<ref name=aod_hp>{{cite web | title =Age of Decadence | publisher =[[Iron Tower Studios]] | url =http://www.irontowerstudio.com/index.htm | format =HTML | accessdate =2007-07-10  }}</ref><ref name=cvg_ss>{{cite web | last =O'Hagan | first =Steve | title =PC Review: Silent Storm | publisher =[[ComputerAndVideoGames.com]] | date =August 7, 2003 | url =http://www.computerandvideogames.com/article.php?id=94816 | format =HTML | accessdate =2007-12-13  }}</ref>, are sometimes referred to as being isometric, or "pseudo-isometric", due to visual similarities or similarities in how the game allows a greater field of view over a large playing field. In the case of games that use perspective projection, "[[bird's-eye view]]" might be a more appropriate term.
+Increasingly, the term is being applied to games that don't use any form of axonometric projection.{{fact}} Games that use [[oblique projection]]<ref name=zelda_gdc>{{cite web | title =GDC 2004: The History of Zelda | publisher =[[IGN]] | date =March 25, 2004 | url =http://cube.ign.com/articles/501/501970p1.html | format =HTML | accessdate =2007-12-17  }}</ref><ref name=gamasutra_uol>{{cite web | last =Greely | first =Dave  | coauthors =Ben Sawyer | title =Has Origin Created the First True Online Game World? | publisher =[[Gamasutra]] | date =August 19, 1997 | url =http://www.gamasutra.com/features/19970819/sawyer_01.htm | format =HTML | accessdate =2007-12-17  }}</ref>, as well as games that use [[perspective projection]]<ref name=aod_hp>{{cite web | title =Age of Decadence | publisher =[[Iron Tower Studios]] | url =http://www.irontowerstudio.com/index.htm | format =HTML | accessdate =2007-07-10  }}</ref><ref name=cvg_ss>{{cite web | last =O'Hagan | first =Steve | title =PC Review: Silent Storm | publisher =[[ComputerAndVideoGames.com]] | date =August 7, 2003 | url =http://www.computerandvideogames.com/article.php?id=94816 | format =HTML | accessdate =2007-12-13  }}</ref>, are sometimes referred to as being isometric, or "pseudo-isometric", due to visual similarities or similarities in how the game allows a greater field of view over a large playing field. In the case of games that use perspective projection, "[[bird's-eye view]]" might be a more appropriate term.
 ==Notable examples of "isometric" computer and video games==

THC Science

Bringing Science to the Cannabis Conversation!

Trichome

Revision as of 19:24, 17 December 2007