Physics B‑class High‑importance

This article is within the scope of WikiProject Physics, a collaborative effort to improve the coverage of Physics on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.PhysicsWikipedia:WikiProject PhysicsTemplate:WikiProject Physicsphysics articles B This article has been rated as B-class on Wikipedia's content assessment scale. High This article has been rated as High-importance on the project's importance scale.

Archives

Archive 1 (2005—2008) Archive 2 (2009—)

What is the wavelength of this wave? 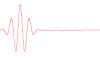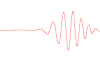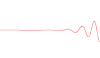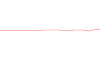What is the exact definion of wavelength? By Fourier Analysis? ––虞海 (Yú Hǎi) 17:37, 10 October 2010 (UTC)[reply]

Is that a meaningful question? What do the authorities define as "wavelength" ? --Wtshymanski (talk) 17:56, 10 October 2010 (UTC)[reply]

Please, per wp:talk page guidelines, take this to the wp:reference desk/science? Thanks. DVdm (talk) 18:09, 10 October 2010 (UTC)[reply]

It doesn't sound like a ref desk question to me, but rather a rhetorical question to see whether we have included a correct and working definition. I don't know of a definition based on Fourier analysis, but there are many alternatives, and maybe one of those, too. Some definitions are predicated on the wave being periodic; others on it being sinusoidal. The "distance between peaks or troughs" definition is usually adequate, and would give a sensible answer for the wave in question, but it may not be both precise and general enough to cover all things that people call wavelength. Dicklyon (talk) 19:57, 10 October 2010 (UTC)[reply]

For slowly-varying and coherent wave trains a good definition is the one by Whitham (see e.g. his book Linear and nonlinear waves) through the definition of the wavenumber as the gradient of the carrier-wave phase θ(x,t): k=∇θ, so λ=2π/|k|. The wave phase of the carrier wave is obtainable through the Hilbert transform of the band-pass filtered signal (removing nonlinear sub- and super-harmonics). -- Crowsnest (talk) 22:05, 10 October 2010 (UTC)[reply]

It's not even clear that this is a meaningful question. Not all waveforms have "a wavelength". General waveforms are composed of a spectrum of waves at different frequencies. One can only define an overall wavelength for a waveform in special cases.

Be sure to read Archive 2 of this talk page (link above). This kind of question has been discussed here before.--Srleffler (talk) 23:09, 10 October 2010 (UTC)[reply]

Ha! That's not likely to be a productive use of time. I like the definition that Crowsnest came up with, though. It works well for any wave that's remotely like sinusoidal. Dicklyon (talk) 23:16, 10 October 2010 (UTC)[reply]

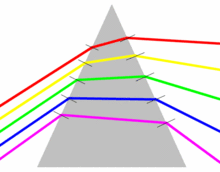
this edit removed the figure at the right with the explanation:

"Rm disputed image altogether. It is not really relevant to the topic here. We are more interested in change in velocity as a function of frequency than in change of direction."

The figure was part of the section discussing dispersion:

the relationship between ω and λ (or k) is called a dispersion relation.

So the topic is the change in the relation between ω and λ introduced by the refractive index of a medium, as indicated in the lower figure. The connection to the prism is via the Fresnel equations which explain that the angle of refraction varies with the refractive index, and thus, when n = n(λ), different colors are refracted by different angles according to Snell's law:

The inclusion of this point is of interest because the separation of colors using a prism is a well-known phenomenon, and its introduction here provides a useful connection for the reader to these topics. It is one of WP's most admired features that it serves to broaden the reader's concept of a topic by pointing out exactly such connections.

On this basis, I'd suggest the reintroduction of this figure with a better explanation and some links to the relevant WP articles on the related topics. Brews ohare (talk) 13:47, 2 April 2012 (UTC)[reply]

I have made an attempt at incorporating this suggestion. Brews ohare (talk) 18:32, 2 April 2012 (UTC)[reply]

If we are going to include an image of a prism dispersing light, it should be the one showing moving waves, because the topic of this article is wavelength, and the relevant effect is that dispersion causes waves with different wavelengths to move with different velocities in the medium. It is interesting that this is related to the angle of refraction, but the latter is not directly relevant to the topic of this article. --Srleffler (talk) 03:53, 3 April 2012 (UTC)[reply]

I removed the details about Snell's law and re-introduced links to the article on dispersion. The fact that prism dispersion is connected with change in wavelength in a medium is interesting and relevant. The details of how to calculate angle of dispersion in a prism are not relevant, and should be found in the linked articles if a reader is interested.

I restored the image that actually shows waves moving with different speeds in a prism, connected with dispersion of light in that prism, because that is the relevant phenomenon here.--Srleffler (talk) 04:54, 3 April 2012 (UTC)[reply]

I moved the discussion of refraction from an earlier section down to this one and modified the text a bit to fit it in more smoothly. Brews ohare (talk) 13:43, 3 April 2012 (UTC)[reply]

This topic may seem to be a digression in the article on wavelength. I am unsure how to handle it, but it shouldn't be ignored altogether. One aspect is shown in the figure: the wavelength of an envelope function differs from that of the constituents and moves at a different speed. Brews ohare (talk) 15:14, 3 April 2012 (UTC)[reply]

DickLyon: This material is not "off-topic bloat". It is relevant for several reasons. Perhaps the main reason is that it points out the wavelength of a combination waveform is not that of its constituents. Another reason is that the this section concerns effects of the dependence of speed of propagation upon wavelength, and this phenomena is one of those consequences. Brews ohare (talk) 18:02, 3 April 2012 (UTC)[reply]

As we discussed at length, years ago, the application of the term "wavelength" to the modulation is rare and unusual, dare I say idiosyncratic. And there are much better places to discuss phase velocity and group velocity than an article on wavelength, which already goes off on too many tangents. Dicklyon (talk) 20:04, 3 April 2012 (UTC)[reply]

Indeed "wavelength" is hardly ever used for this: I know it under the names group length, modulation length or envelope length. -- Crowsnest (talk) 20:53, 3 April 2012 (UTC)[reply]

Crowsnest: Thanks for those links that establish some terminology I was unaware of. It does seem, however, that if one has an envelope f that satisfies the normal definition of a periodic function, that is,

with ξ = x-vt there is no doubt whatsoever that the normal definition of wavelength applies to this envelope function f, whatever name one may attach to the envelope itself. Don't you agree? Brews ohare (talk) 21:39, 3 April 2012 (UTC)[reply]

It's logical that the term could apply, but it's seldom or never used that way, so let's not. Dicklyon (talk) 00:27, 4 April 2012 (UTC)[reply]

The terms "group length", modulation length" and "envelope length" definitely are used to apply to the length of a wave packet, but I haven't found them used for a periodic envelope like that in the image above. In any event, it is not only "logical" to use the term wavelength in connection with a periodic envelope function, it is mathematically perfectly and completely correct according to the definition of a periodic function. Brews ohare (talk) 01:28, 4 April 2012 (UTC)[reply]

Wikipedia relies on sources, not logic. Our role is to report what is documented in reliable sources, not to synthesize our own knowledge, even when that knowledge follows logically from the source materials. See Wikipedia:No original research and WP:SYNTHESIS for more on this.--Srleffler (talk) 03:10, 4 April 2012 (UTC)[reply]

That is of course absurd; if we didn't use logic, we'd be forced to make word for word copies of sources. --Wtshymanski (talk) 03:35, 4 April 2012 (UTC)[reply]

Brews is arguing that we should cover a usage of a term purely because it is a logical extension of the usual definition, despite admitting that he hasn't found any sources that use the term that way. This is pretty clearly not allowed by policy.--Srleffler (talk) 04:37, 4 April 2012 (UTC)[reply]

There is no "logical extension" of the definition of wavelength involved here. If a function f satisfies

then λ is its wavelength. Period. The only point to discuss is whether periodic envelopes are worth mentioning. I'd guess that DickLyon and Srleffler would say "No, it is an uninteresting topic". Dismissing the matter on spurious grounds simply avoids the real basis for discussion. Brews ohare (talk) 05:46, 4 April 2012 (UTC)[reply]

Some references are: Stade and Holbrow et al. Brews ohare (talk) 15:07, 4 April 2012 (UTC)[reply]

Your first ref is not about waves, and the second is about sinusoidal waves; so what's your point? Dicklyon (talk) 15:33, 4 April 2012 (UTC)[reply]

Shouldn't all the discussion about propagation, dispersion, and other properties of waves be left to the article Wave? That would turn this article into a dictdef that could be moved to Wiktionary. --Wtshymanski (talk) 14:46, 4 April 2012 (UTC)[reply]

Wavelength is a property of waves, and it is sufficiently complicated to require its own article rather than loading down Wave. Brews ohare (talk) 15:07, 4 April 2012 (UTC)[reply]

We need the right compromise. There's a lot to say about wavelength, and we've pretty much said that and more. Other stuff is better off in an article on waves. Dicklyon (talk) 15:33, 4 April 2012 (UTC)[reply]

The article in its present form describes wavelength using a sine wave image and generalizes this simple case with the remark:

The concept can also be applied to periodic waves of non-sinusoidal shape

A more fundamental and rigorous approach would be to point out that a Fourier series assembled from sinusoidal functions of the form:

(n a positive integer) in the form:

represents any (bounded and integrable) function in the interval −λ/2 ≤ ξ < λ/2. This function has the property that it repeats periodically in ξ as described by:

where λ is variously called the period or the wavelength of the function. By choosing

where x is distance along an axis in space and t is time, the function f describes a waveform with wavelength λ propagating with time-invariant shape in the positive x direction with a velocity v.

References

• Eric Stade (2011). Fourier Analysis. John Wiley & Sons. p. 3. ISBN 1118165519.
• Gerald B Folland (2009). "Chapter 2: Fourier Series". Fourier Analysis and Its Applications. American Mathematical Society. pp. 18 ff. ISBN 0821847902.

I don't think this description need appear in the introduction, but perhaps in the section Mathematical representation. It should appear in Wavelength because it is a general concept of wavelength for waves of arbitrary shape, and makes the connection to Fourier series, which is an important idea in the theory of waves that the reader should become aware of. Brews ohare (talk) 16:28, 4 April 2012 (UTC)[reply]