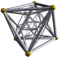
→One dimension: YES! Reg Poly. p.129 {{fact|date=January 2015|reason=Did Coxeter really use the symbol { }?}} |
|||
| Line 40: | Line 40: | ||
==One dimension== |
==One dimension== |
||
The closed [[line segment]], bounded by its two endpoints, is sometimes treated as a one-dimensional polytope. It can be represented by [[Schläfli symbol]] { }, and [[Coxeter diagram]], {{CDD|node_1}}. |
The closed [[line segment]], bounded by its two endpoints, is sometimes treated as a one-dimensional polytope. It can be represented by [[Schläfli symbol]] { }<ref>Regular polytopes, p. 129<ref>, and can be called a ''ditel''<ref>http://www.foibg.com/ibs_isc/ibs-25/ibs-25-p07.pdf</ref>, and [[Coxeter diagram]], {{CDD|node_1}}. Although trivial as a polytope, it appears as the [[Edge (geometry)|edges]] of higher dimensional polytopes.<ref>Regular polytopes, p. 120</ref> It is used in the definition of [[prism (geometry)|uniform prism]]s like Schläfli symbol { }×{p}, or Coxeter diagram {{CDD|node_1|2|node_1|p|node}} as a [[Cartesian product]] of a line segment and a regular polygon.<ref>Regular polytopes, p. 124</ref> |
||
== Two dimensions (polygons) == |
== Two dimensions (polygons) == |
||
Revision as of 19:46, 12 January 2015
This page lists the regular polytopes in Euclidean, spherical and hyperbolic spaces. The Schläfli symbol notation describes every regular polytope, and is used widely below as a compact reference name for each.
The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.
Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with 7 equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.
Overview
This table shows a summary of regular polytope counts by dimension.
| Dimension | Convex | Star | Convex Euclidean tessellations |
Compact hyperbolic tessellations |
Star hyperbolic tessellations |
Paracompact hyperbolic tessellations |
Abstract Polytopes |
|---|---|---|---|---|---|---|---|
| 1 | 1 line segment | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | ∞ polygons | ∞ star polygons | 1 | 1 | 0 | 0 | ∞ |
| 3 | 5 Platonic | 4 Kepler–Poinsot | 3 tilings | ∞ | ∞ | ∞ | ∞ |
| 4 | 6 4-polytopes | 10 Schläfli–Hess | 1 3-honeycombs | 4 | 0 | 11 | ∞ |
| 5 | 3 5-polytopes | 0 | 3 4-honeycombs | 5 | 4 | 2 | ∞ |
| 6 | 3 6-polytopes | 0 | 1 5-honeycombs | 0 | 0 | 5 | ∞ |
| 7+ | 3 | 0 | 1 | 0 | 0 | 0 | ∞ |
There are no nonconvex Euclidean regular tessellations in any number of dimensions.
Tessellations
The classical convex polytopes may be considered tessellations, or tilings, of spherical space. Tessellations of euclidean and hyperbolic space may also be considered regular polytopes. Note that an 'n'-dimensional polytope actually tessellates a space of one dimension less. For example, the (three-dimensional) platonic solids tessellate the 'two'-dimensional 'surface' of the sphere.
One dimension
The closed line segment, bounded by its two endpoints, is sometimes treated as a one-dimensional polytope. It can be represented by Schläfli symbol { }Cite error: A <ref> tag is missing the closing </ref> (see the help page)., and Coxeter diagram, ![]() . Although trivial as a polytope, it appears as the edges of higher dimensional polytopes.[1] It is used in the definition of uniform prisms like Schläfli symbol { }×{p}, or Coxeter diagram
. Although trivial as a polytope, it appears as the edges of higher dimensional polytopes.[1] It is used in the definition of uniform prisms like Schläfli symbol { }×{p}, or Coxeter diagram ![]()
![]()
![]()
![]()
![]() as a Cartesian product of a line segment and a regular polygon.[2]
as a Cartesian product of a line segment and a regular polygon.[2]
Two dimensions (polygons)
The two-dimensional polytopes are called polygons. Regular polygons are equilateral and cyclic. A p-gonal regular polygon is represented by Schläfli symbol {p}.
Usually only convex polygons are considered regular, but star polygons, like the pentagram, can also be considered regular. They use the same vertices as the convex forms, but connect in an alternate connectivity which passes around the circle more than once to complete.
Star polygons should be called nonconvex rather than concave because the intersecting edges do not generate new vertices and all the vertices exist on a circle boundary.
Convex
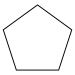
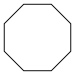
The Schläfli symbol {p} represents a regular p-gon.
| Name | Triangle (2-simplex) |
Square (2-orthoplex) (2-cube) |
Pentagon | Hexagon | Heptagon | Octagon | |
|---|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} | {5} | {6} | {7} | {8} | |
| Coxeter | |||||||
| Image | 
|

|
|

|

|
| |
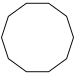
| Name | Enneagon | Decagon | Hendecagon | Dodecagon | Tridecagon | Tetradecagon | |
| Schläfli | {9} | {10} | {11} | {12} | {13} | {14} | |
| Dynkin | |||||||
| Image | 
|
|
|

|
|

| |
| Name | Pentadecagon | Hexadecagon | Heptadecagon | Octadecagon | Enneadecagon | Icosagon | ...p-gon |
| Schläfli | {15} | {16} | {17} | {18} | {19} | {20} | {p} |
| Dynkin | |||||||
| Image | 
|
|
|

|
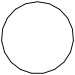
|

|
Improper (spherical)
The regular monogon {1} and regular digon {2} can be considered degenerate regular polygons. They can exist in non-Euclidean spaces like on the surface of a sphere or torus.
| Name | Monogon | Digon |
|---|---|---|
| Schläfli symbol | {1} | {2} |
| Coxeter diagram | ||
| Image | 
|

|
Non-convex
There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are called star polygons and share the same vertex arrangements of the convex regular polygons.
In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime.
| Name | Pentagram | Heptagrams | Octagram | Enneagrams | Decagram | ...n-agrams | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {p/q} |
| Coxeter | ||||||||
| Image | 
|

|

|
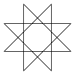
|
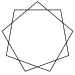
|
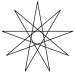
|

|
|
Tessellations
There is one tessellation of the line, giving one polytope, the (two-dimensional) apeirogon (aze). This has infinitely many vertices and edges. Its Schläfli symbol is {∞}, and Coxeter diagram ![]()
![]()
![]() .
.
Three dimensions (polyhedra)
In three dimensions, polytopes are called polyhedra:
A regular polyhedron with Schläfli symbol {p,q}, Coxeter diagrams ![]()
![]()
![]()
![]()
![]() , has a regular face type {p}, and regular vertex figure {q}.
, has a regular face type {p}, and regular vertex figure {q}.
A vertex figure (of a polyhedron) is a polygon, seen by connecting those vertices which are one edge away from a given vertex. For regular polyhedra, this vertex figure is always a regular (and planar) polygon.
Existence of a regular polyhedron {p,q} is constrained by an inequality, related to the vertex figure's angle defect:
- : Polyhedron (existing in Euclidean 3-space)
- : Euclidean plane tiling
- : Hyperbolic plane tiling
By enumerating the permutations, we find 5 convex forms, 4 star forms and 3 plane tilings, all with polygons {p} and {q} limited to: {3}, {4}, {5}, {5/2}, and {6}.
Beyond Euclidean space, there is an infinite set of regular hyperbolic tilings.
Convex
The convex regular polyhedra are called the 5 Platonic solids. The vertex figure is given with each vertex count. All these polyhedra have an Euler characteristic (χ) of 2.
| Name | Schläfli {p,q} |
Coxeter |
Image (transparent) |
Image (solid) |
Image (sphere) |
Faces {p} |
Edges | Vertices {q} |
Symmetry | Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedron (3-simplex) |
{3,3} | 
|

|

|
4 {3} |
6 | 4 {3} |
Td [3,3] (*332) |
(self) | |
| Hexahedron Cube (3-cube) |
{4,3} | 
|

|

|
6 {4} |
12 | 8 {3} |
Oh [4,3] (*432) |
Octahedron | |
| Octahedron (3-orthoplex) |
{3,4} | 
|

|

|
8 {3} |
12 | 6 {4} |
Oh [4,3] (*432) |
Cube | |
| Dodecahedron | {5,3} | 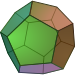
|

|
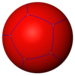
|
12 {5} |
30 | 20 {3} |
Ih [5,3] (*532) |
Icosahedron | |
| Icosahedron | {3,5} | 
|

|

|
20 {3} |
30 | 12 {5} |
Ih [5,3] (*532) |
Dodecahedron |
Improper (spherical)
In spherical geometry, regular spherical polyhedra (tilings of the sphere) exist that would otherwise be degenerate as polytopes. These are the hosohedra {2,n}, their dual dihedra {n,2} and monohedron {1,1}. Coxeter calls these cases "improper" tessellations.[3]
Some include:
| Name | Schläfli {p,q} |
Coxeter diagram |
Image (sphere) |
Faces {p} |
Edges { } |
Vertices {q} |
Symmetry | Dual |
|---|---|---|---|---|---|---|---|---|
| Monohedron (half monogonal hosohedron) |
{1,1} =h{2,1} |

|
1 {1} |
0 { } |
1 {1} |
C1v [ ] (*1) |
Self | |
| Monogonal hosohedron | {2,1} | 
|
1 {2} |
1 { } |
2 {1} |
D1h [2,1] (*22) |
Monogonal dihedron | |
| Digonal hosohedron (Same as digonal dihedron) |
{2,2} | 
|
2 {2} |
2 { } |
2 {2} |
D2h [2,2] (*222) |
Self | |
| Trigonal hosohedron | {2,3} | 
|
3 {2} |
3 { } |
2 {3} |
D3h [2,3] (*322) |
Trigonal dihedron | |
| Square hosohedron | {2,4} | 
|
4 {2} |
4 { } |
2 {4} |
D4h [2,4] (*422) |
Square dihedron | |
| Pentagonal hosohedron | {2,5} | 
|
5 {2} |
5 { } |
2 {5} |
D5h [2,5] (*522) |
Pentagonal dihedron | |
| Hexagonal hosohedron | {2,6} | 
|
6 {2} |
6 { } |
2 {6} |
D6h [2,6] (*622) |
Hexagonal dihedron | |
| Monogonal dihedron (half monogonal hosohedron) |
{1,2} =h{2,2} |

|
2 {1} |
1 { } |
1 {2} |
D1h [1,2] (*22) |
Monogonal hosohedron | |
| Digonal dihedron (Same as digonal hosohedron) |
{2,2} | 
|
2 {2} |
2 { } |
2 {2} |
D2h [2,2] (*222) |
Self | |
| Trigonal dihedron | {3,2} | 
|
2 {3} |
3 { } |
3 {2} |
D3h [3,2] (*322) |
Trigonal hosohedron | |
| Square dihedron | {4,2} | 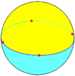
|
2 {4} |
4 { } |
4 {2} |
D4h [4,2] (*422) |
Square hosohedron | |
| Pentagonal dihedron | {5,2} | 2 {5} |
5 { } |
5 {2} |
D5h [5,2] (*522) |
Pentagonal hosohedron | ||
| Hexagonal dihedron | {6,2} | 
|
2 {6} |
6 { } |
6 {2} |
D6h [6,2] (*622) |
Hexagonal hosohedron |
Non-convex
The regular star polyhedra are called the Kepler–Poinsot polyhedra and there are four of them, based on the vertex arrangements of the dodecahedron {5,3} and icosahedron {3,5}:
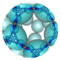
As spherical tilings, these nonconvex forms overlap the sphere multiple times, called its density, being 3 or 7 for these forms. The tiling images show a single spherical polygon face in yellow.
| Name | Image (transparent) |
Image (solid) |
Image (sphere) |
Stellation diagram |
Schläfli {p,q} and Coxeter |
Faces {p} |
Edges | Vertices {q} verf. |
χ | Density | Symmetry | Dual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Small stellated dodecahedron | 
|

|

|

|
{5/2,5} |
12 {5/2} |
30 | 12 {5} |
−6 | 3 | Ih [5,3] (*532) |
Great dodecahedron |
| Great dodecahedron | 
|

|

|

|
{5,5/2} |
12 {5} |
30 | 12 {5/2} |
−6 | 3 | Ih [5,3] (*532) |
Small stellated dodecahedron |
| Great stellated dodecahedron | 
|

|

|

|
{5/2,3} |
12 {5/2} |
30 | 20 {3} |
2 | 7 | Ih [5,3] (*532) |
Great icosahedron |
| Great icosahedron | 
|

|

|

|
{3,5/2} |
20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih [5,3] (*532) |
Great stellated dodecahedron |
Tessellations
Euclidean tilings
There are three regular tessellations of the plane. All three have an Euler characteristic (χ) of 0.
| Name | Square tiling (quadrille) |
Triangular tiling (deltille) |
Hexagonal tiling (hextille) |
|---|---|---|---|
| Symmetry | p4m, [4,4] | p6m, [6,3] | |
| Schläfli {p,q} | {4,4} | {3,6} | {6,3} |
| Coxeter diagram | |||
| Image | 
|

|

|
| Symmetry | *442 (p4m) |
*632 (p6m) | |
There is one degenerate regular tiling, {∞,2} (azat), made from two apeirogons, each filling half the plane. This tiling is related to a 2-faced dihedron, {p,2}, on the sphere.
Euclidean star-tilings
There are no regular plane tilings of star polygons. There are many enumerations that fit in the plane (1/p + 1/q = 1/2), like {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, etc., but none repeat periodically.
Hyperbolic tilings
Tessellations of hyperbolic 2-space can be called hyperbolic tilings. There are infinitely many regular tilings in H2. As stated above, every positive integer pair {p,q} such that 1/p + 1/q < 1/2 gives a hyperbolic tiling. In fact, for the general Schwarz triangle (p, q, r) the same holds true for 1/p + 1/q + 1/r < 1.
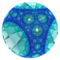
There are a number of different ways to display the hyperbolic plane, including the Poincaré disc model which maps the plane into a circle, as shown below. It should be recognized that all of the polygon faces in the tilings below are equal-sized and only appear to get smaller near the edges due to the projection applied, very similar to the effect of a camera fisheye lens.
A sampling:
| Regular hyperbolic tiling table | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical (improper/Platonic)/Euclidean/hyperbolic (Poincaré disc: compact/paracompact/noncompact) tessellations with their Schläfli symbol | |||||||||||
| p \ q | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 2 |  {2,2} |
 {2,3} |
 {2,4} |
 {2,5} |
 {2,6} |
 {2,7} |
 {2,8} |
 {2,∞} |
 {2,iπ/λ} | ||
| 3 |  {3,2} |
 (tetrahedron) {3,3} |
 (octahedron) {3,4} |
 (icosahedron) {3,5} |
 (deltille) {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} |
 {3,iπ/λ} | ||
| 4 | 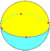 {4,2} |
 (cube) {4,3} |
 (quadrille) {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
 {4,∞} |
 {4,iπ/λ} | ||
| 5 |  {5,2} |
 (dodecahedron) {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
 {5,7} |
 {5,8} |
 {5,∞} |
 {5,iπ/λ} | ||
| 6 |  {6,2} |
 (hextille) {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
 {6,∞} |
 {6,iπ/λ} | ||
| 7 | {7,2} |
 {7,3} |
 {7,4} |
 {7,5} |
 {7,6} |
 {7,7} |
{7,8} |
 {7,∞} |
{7,iπ/λ} | ||
| 8 | {8,2} |
 {8,3} |
 {8,4} |
 {8,5} |
 {8,6} |
 {8,7} |
 {8,8} |
 {8,∞} |
{8,iπ/λ} | ||
| ... | |||||||||||
| ∞ |  {∞,2} |
 {∞,3} |
 {∞,4} |
 {∞,5} |
 {∞,6} |
 {∞,7} |
 {∞,8} |
 {∞,∞} |
 {∞,iπ/λ} | ||
| ... | |||||||||||
| iπ/λ |  {iπ/λ,2} |
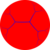 {iπ/λ,3} |
 {iπ/λ,4} |
 {iπ/λ,5} |
 {iπ/λ,6} |
{iπ/λ,7} |
{iπ/λ,8} |
 {iπ/λ,∞} |

{iπ/λ, iπ/λ} | ||
Hyperbolic star-tilings
There are 2 infinite forms of hyperbolic tilings whose faces or vertex figures are star polygons: {m/2, m} and their duals {m, m/2} with m = 7, 9, 11, .... The {m/2, m} tilings are stellations of the {m, 3} tilings while the {m, m/2} dual tilings are facetings of the {3, m} tilings and greatenings of the {m, 3} tilings.
The patterns {m/2, m} and {m, m/2} continue for odd m < 7 as polyhedra: when m = 5, we obtain the small stellated dodecahedron and great dodecahedron, and when m = 3, we obtain the tetrahedron. If m is even, depending on how we choose to define {m/2}, we can either obtain degenerate double covers of other tilings or compound tilings.
| Name | Schläfli | Coxeter diagram | Image | Face type {p} |
Vertex figure {q} |
Density | Symmetry | Dual |
|---|---|---|---|---|---|---|---|---|
| Order-7 heptagrammic tiling | {7/2,7} | 
|
{7/2} |
{7} |
3 | *732 | Heptagrammic-order heptagonal tiling | |
| Heptagrammic-order heptagonal tiling | {7,7/2} | 
|
{7} |
{7/2} |
3 | *732 | Order-7 heptagrammic tiling | |
| Order-9 enneagrammic tiling | {9/2,9} | 
|
{9/2} |
{9} |
3 | *932 | Enneagrammic-order enneagonal tiling | |
| Enneagrammic-order enneagonal tiling | {9,9/2} | 
|
{9} |
{9/2} |
3 | *932 | Order-9 enneagrammic tiling | |
| Order-p p-grammic tiling | {p/2,p} | {p/2} | {p} | 3 | *p32 | p-grammic-order p-gonal tiling | ||
| p-grammic-order p-gonal tiling | {p,p/2} | {p} | {p/2} | 3 | *p32 | Order-p p-grammic tiling |
Four dimensions
Regular 4-polytopes with Schläfli symbol have cells of type , faces of type , edge figures , and vertex figures .
- A vertex figure (of a 4-polytope) is a polyhedron, seen by the arrangement of neighboring vertices around a given vertex. For regular polychora, this vertex figure is a regular polyhedron.
- An edge figure is a polygon, seen by the arrangement of faces around an edge. For regular polychora, this edge figure will always be a regular polygon.
The existence of a regular 4-polytope is constrained by the existence of the regular polyhedra .
Each will exist in a space dependent upon this expression:
-
- : Hyperspherical 3-space honeycomb or 4-polytope
- : Euclidean 3-space honeycomb
- : Hyperbolic 3-space honeycomb
These constraints allow for 21 forms: 6 are convex, 10 are nonconvex, one is a Euclidean 3-space honeycomb, and 4 are hyperbolic honeycombs.
The Euler characteristic for polychora is and is zero for all forms.
Convex
The 6 convex regular 4-polytopes are shown in the table below. All these polychora have an Euler characteristic (χ) of 0.
| Name |
Schläfli {p,q,r} |
Coxeter |
Cells {p,q} |
Faces {p} |
Edges {r} |
Vertices {q,r} |
Dual {r,q,p} |
|---|---|---|---|---|---|---|---|
| 5-cell (4-simplex) (Pentachoron) (pen) |
{3,3,3} | 5 {3,3} |
10 {3} |
10 {3} |
5 {3,3} |
(self) | |
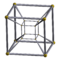
| 8-cell (4-cube) (Tesseract) (tes) |
{4,3,3} | 8 {4,3} |
24 {4} |
32 {3} |
16 {3,3} |
16-cell | |
| 16-cell (4-orthoplex) (hex) |
{3,3,4} | 16 {3,3} |
32 {3} |
24 {4} |
8 {3,4} |
Tesseract | |
| 24-cell (ico) |
{3,4,3} | 24 {3,4} |
96 {3} |
96 {3} |
24 {4,3} |
(self) | |
| 120-cell (hi) |
{5,3,3} | 120 {5,3} |
720 {5} |
1200 {3} |
600 {3,3} |
600-cell | |
| 600-cell (ex) |
{3,3,5} | 600 {3,3} |
1200 {3} |
720 {5} |
120 {3,5} |
120-cell |
| 5-cell | 8-cell | 16-cell | 24-cell | 120-cell | 600-cell |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Wireframe (Petrie polygon) skew orthographic projections | |||||

|

|
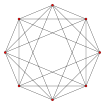
|
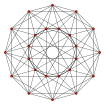
|

|

|
| Solid orthographic projections | |||||
 tetrahedral envelope (cell/vertex-centered) |
 cubic envelope (cell-centered) |
 Cubic envelope (cell-centered) |
 cuboctahedral envelope (cell-centered) |
 truncated rhombic triacontahedron envelope (cell-centered) |
 Pentakis icosidodecahedral envelope (vertex-centered) |
| Wireframe Schlegel diagrams (Perspective projection) | |||||
 (Cell-centered) |
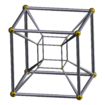 (Cell-centered) |
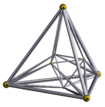 (Cell-centered) |
 (Cell-centered) |
 (Cell-centered) |
 (Vertex-centered) |
| Wireframe stereographic projections (Hyperspherical) | |||||

|
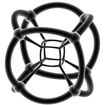
|

|

|

|

|
Improper (spherical)
Dichora and hosochora exist as regular tessellations of the 3-sphere.
Regular dichora (2 facets) include: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, and their hosochora duals (2 vertices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Polychora of the form {2,p,2} are both dichora and hosochora.
Non-convex
There are ten regular star 4-polytopes, which are called the Schläfli–Hess 4-polytopes. Their vertices are based on the convex 120-cell {5,3,3} and 600-cell {3,3,5}.
Ludwig Schläfli found four of them and skipped the last six because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: F+V−E=2). Edmund Hess (1843–1903) completed the full list of ten in his German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (1883)[1].
There are 4 unique edge arrangements and 7 unique face arrangements from these 10 nonconvex polychora, shown as orthogonal projections:
| Name |
Wireframe | Solid | Schläfli {p, q, r} Coxeter |
Cells {p, q} |
Faces {p} |
Edges {r} |
Vertices {q, r} |
Density | χ | Symmetry group | Dual {r, q,p} |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Icosahedral 120-cell (faceted 600-cell) (fix) |

|

|
{3,5,5/2} |
120 {3,5} |
1200 {3} |
720 {5/2} |
120 {5,5/2} |
4 | 480 | H4 [5,3,3] |
Small stellated 120-cell |
| Small stellated 120-cell (sishi) |

|

|
{5/2,5,3} |
120 {5/2,5} |
720 {5/2} |
1200 {3} |
120 {5,3} |
4 | −480 | H4 [5,3,3] |
Icosahedral 120-cell |
| Great 120-cell (gohi) |

|

|
{5,5/2,5} |
120 {5,5/2} |
720 {5} |
720 {5} |
120 {5/2,5} |
6 | 0 | H4 [5,3,3] |
Self-dual |
| Grand 120-cell (gahi) |

|

|
{5,3,5/2} |
120 {5,3} |
720 {5} |
720 {5/2} |
120 {3,5/2} |
20 | 0 | H4 [5,3,3] |
Great stellated 120-cell |
| Great stellated 120-cell (gishi) |

|

|
{5/2,3,5} |
120 {5/2,3} |
720 {5/2} |
720 {5} |
120 {3,5} |
20 | 0 | H4 [5,3,3] |
Grand 120-cell |
| Grand stellated 120-cell (gashi) |

|

|
{5/2,5,5/2} |
120 {5/2,5} |
720 {5/2} |
720 {5/2} |
120 {5,5/2} |
66 | 0 | H4 [5,3,3] |
Self-dual |
| Great grand 120-cell (gaghi) |

|

|
{5,5/2,3} |
120 {5,5/2} |
720 {5} |
1200 {3} |
120 {5/2,3} |
76 | −480 | H4 [5,3,3] |
Great icosahedral 120-cell |
| Great icosahedral 120-cell (great faceted 600-cell) (gofix) |

|

|
{3,5/2,5} |
120 {3,5/2} |
1200 {3} |
720 {5} |
120 {5/2,5} |
76 | 480 | H4 [5,3,3] |
Great grand 120-cell |
| Grand 600-cell (gax) |

|

|
{3,3,5/2} |
600 {3,3} |
1200 {3} |
720 {5/2} |
120 {3,5/2} |
191 | 0 | H4 [5,3,3] |
Great grand stellated 120-cell |
| Great grand stellated 120-cell (gogishi) |

|

|
{5/2,3,3} |
120 {5/2,3} |
720 {5/2} |
1200 {3} |
600 {3,3} |
191 | 0 | H4 [5,3,3] |
Grand 600-cell |
There are 4 failed potential nonconvex regular polychora permutations: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Their cells and vertex figures exist, but they do not cover a hypersphere with a finite number of repetitions.
Tessellations of Euclidean 3-space

There is only one non-degenerate regular tessellation of 3-space (honeycombs):
| Name | Schläfli {p,q,r} |
Coxeter |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure {q,r} |
χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Cubic honeycomb (chon) |
{4,3,4} | {4,3} | {4} | {4} | {3,4} | 0 | Self-dual |
Improper tessellations of Euclidean 3-space

There are six improper regular tessellations, pairs based on the three regular Euclidean tilings. Their cells and vertex figures are all regular hosohedra {2,n}, dihedra, {n,2}, and Euclidean tilings. These improper regular tilings are constructionally related to prismatic uniform honeycombs by truncation operations. They are higher-dimensional analogues of the order-2 apeirogonal tiling and apeirogonal hosohedron.
| Schläfli {p,q,r} |
Coxeter diagram |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure {q,r} |
|---|---|---|---|---|---|
| {2,4,4} | {2,4} | {2} | {4} | {4,4} | |
| {2,3,6} | {2,3} | {2} | {6} | {3,6} | |
| {2,6,3} | {2,6} | {2} | {3} | {6,3} | |
| {4,4,2} | {4,4} | {4} | {2} | {4,2} | |
| {3,6,2} | {3,6} | {3} | {2} | {6,2} | |
| {6,3,2} | {6,3} | {6} | {2} | {3,2} |
Tessellations of hyperbolic 3-space
| ||||
|
Tessellations of hyperbolic 3-space can be called hyperbolic honeycombs. There are 15 hyperbolic honeycombs in H3, 4 compact and 11 paracompact.
| Name | Schläfli Symbol {p,q,r} |
Coxeter |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure {q,r} |
χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Icosahedral honeycomb | {3,5,3} | {3,5} | {3} | {3} | {5,3} | 0 | Self-dual | |
| Order-5 cubic honeycomb | {4,3,5} | {4,3} | {4} | {5} | {3,5} | 0 | {5,3,4} | |
| Order-4 dodecahedral honeycomb | {5,3,4} | {5,3} | {5} | {4} | {3,4} | 0 | {4,3,5} | |
| Order-5 dodecahedral honeycomb | {5,3,5} | {5,3} | {5} | {5} | {3,5} | 0 | Self-dual |
There are also 11 paracompact H3 honeycombs (those with infinite (Euclidean) cells and/or vertex figures): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}.
| Name | Schläfli Symbol {p,q,r} |
Coxeter |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure {q,r} |
χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Order-6 tetrahedral honeycomb | {3,3,6} | {3,3} | {3} | {6} | {3,6} | 0 | {6,3,3} | |
| Hexagonal tiling honeycomb | {6,3,3} | {6,3} | {6} | {3} | {3,3} | 0 | {3,3,6} | |
| Order-4 octahedral honeycomb | {3,4,4} | {3,4} | {3} | {4} | {4,4} | 0 | {4,4,3} | |
| Square tiling honeycomb | {4,4,3} | {4,4} | {4} | {3} | {4,3} | 0 | {3,3,4} | |
| Triangular tiling honeycomb | {3,6,3} | {3,6} | {3} | {3} | {6,3} | 0 | Self-dual | |
| Order-6 cubic honeycomb | {4,3,6} | {4,3} | {4} | {4} | {3,4} | 0 | {6,3,4} | |
| Order-4 hexagonal tiling honeycomb | {6,3,4} | {6,3} | {6} | {4} | {3,4} | 0 | {4,3,6} | |
| Order-4 square tiling honeycomb | {4,4,4} | {4,4} | {4} | {4} | {4,4} | 0 | {4,4,4} | |
| Order-6 dodecahedral honeycomb | {5,3,6} | {5,3} | {5} | {5} | {3,5} | 0 | {6,3,5} | |
| Order-5 hexagonal tiling honeycomb | {6,3,5} | {6,3} | {6} | {5} | {3,5} | 0 | {5,3,6} | |
| Order-6 hexagonal tiling honeycomb | {6,3,6} | {6,3} | {6} | {6} | {3,6} | 0 | Self-dual |
A subset of uniform polychora and honeycombs are contained in the form {p,3,q} for values 3 to 6. Noncompact solutions exist as Lorentzian Coxeter groups for p or q greater than 6, and can be visualized with open domains in hyperbolic space, and a few are drawn below as tilings on the ideal half-space plane.
| {p,3} \ r | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... ∞ |
|---|---|---|---|---|---|---|---|---|
{2,3}
|
 {2,3,2} |
{2,3,3} | {2,3,4} | {2,3,5} | {2,3,6} | {2,3,7} | {2,3,8} | {2,3,∞} |
{3,3}
|
 {3,3,2} |
 {3,3,3} |
 {3,3,4} |
 {3,3,5} |
 {3,3,6} |
 {3,3,7} |
 {3,3,8} |
 {3,3,∞} |
| {4,3} |
 {4,3,2} |
 {4,3,3} |
 {4,3,4} |
 {4,3,5} |
 {4,3,6} |
 {4,3,7} |
 {4,3,8} |
 {4,3,∞} |
{5,3}
|
 {5,3,2} |
 {5,3,3} |
 {5,3,4} |
 {5,3,5} |
 {5,3,6} |
 {5,3,7} |
 {5,3,8} |
 {5,3,∞} |
{6,3}
|
 {6,3,2} |
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {6,3,7} |
 {6,3,8} |
 {6,3,∞} |
{7,3}
|
{7,3,2} |  {7,3,3} |
 {7,3,4} |
 {7,3,5} |
 {7,3,6} |
 {7,3,7} |
 {7,3,8} |
 {7,3,∞} |
{8,3}
|
{8,3,2} |  {8,3,3} |
 {8,3,4} |
 {8,3,5} |
 {8,3,6} |
 {8,3,7} |
 {8,3,8} |
 {8,3,∞} |
... {∞,3}
|
{∞,3,2} |  {∞,3,3} |
 {∞,3,4} |
 {∞,3,5} |
 {∞,3,6} |
 {∞,3,7} |
 {∞,3,8} |
 {∞,3,∞} |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Five and more dimensions
In five dimensions, a regular polytope can be named as where is the hypercell (or teron) type, is the cell type, is the face type, and is the face figure, is the edge figure, and is the vertex figure.
A 5-polytope has been called a polyteron, and if infinite (i.e. a honeycomb) a tetracomb.
- A vertex figure (of a 5-polytope) is a 4-polytope, seen by the arrangement of neighboring vertices to each vertex.
- An edge figure (of a 5-polytope) is a polyhedron, seen by the arrangement of faces around each edge.
- A face figure (of a 5-polytope) is a polygon, seen by the arrangement of cells around each face.
A regular 5-polytope exists only if and are regular polychora.
The space it fits in is based on the expression:
-
- : Spherical 4-space tessellation or 5-space polytope
- : Euclidean 4-space tessellation
- : hyperbolic 4-space tessellation
Enumeration of these constraints produce 3 convex polytopes, zero nonconvex polytopes, 3 4-space tessellations, and 5 hyperbolic 4-space tessellations. There are no non-convex regular polytopes in five dimensions or higher.
Higher-dimensional polytopes have sometimes received names. 6-polytopes have sometimes been called polypeta, 7-polytopes polyexa, 8-polytopes polyzetta, and 9-polytopes polyyotta.
Convex
In dimensions 5 and higher, there are only three kinds of convex regular polytopes.[4]
| Name | Schläfli Symbol {p1,...,pn−1} |
Coxeter | k-faces | Facet type |
Vertex figure |
Dual |
|---|---|---|---|---|---|---|
| n-simplex | {3n−1} | {3n−2} | {3n−2} | Self-dual | ||
| n-cube | {4,3n−2} | {4,3n−3} | {3n−2} | n-orthoplex | ||
| n-orthoplex | {3n−2,4} | {3n−2} | {3n−3,4} | n-cube |
5 dimensions
| Name | Schläfli Symbol {p,q,r,s} Coxeter |
Facets {p,q,r} |
Cells {p,q} |
Faces {p} |
Edges | Vertices | Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
|---|---|---|---|---|---|---|---|---|---|
| 5-simplex (hix) | {3,3,3,3} |
6 {3,3,3} |
15 {3,3} |
20 {3} |
15 | 6 | {3} | {3,3} | {3,3,3} |
| 5-cube (pent) | {4,3,3,3} |
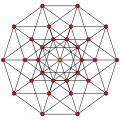
10 {4,3,3} |
40 {4,3} |
80 {4} |
80 | 32 | {3} | {3,3} | {3,3,3} |
| 5-orthoplex (tac) | {3,3,3,4} |
32 {3,3,3} |
80 {3,3} |
80 {3} |
40 | 10 | {4} | {3,4} | {3,3,4} |
 5-simplex |
 5-cube |
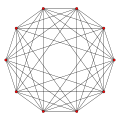 5-orthoplex |
6 dimensions
| Name | Schläfli | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | χ |
|---|---|---|---|---|---|---|---|---|
| 6-simplex (hop) | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 21 | 7 | 0 |
| 6-cube (ax) | {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 0 |
| 6-orthoplex (gee) | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 64 | 0 |
 6-simplex |
 6-cube |
 6-orthoplex |
7 dimensions
| Name | Schläfli | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | χ |
|---|---|---|---|---|---|---|---|---|---|
| 7-simplex (oca) | {3,3,3,3,3,3} | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 2 |
| 7-cube (hept) | {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 2 |
| 7-orthoplex (zee) | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 2 |
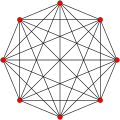 7-simplex |
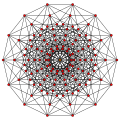 7-cube |
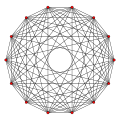 7-orthoplex |
8 dimensions
| Name | Schläfli | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | χ |
|---|---|---|---|---|---|---|---|---|---|---|
| 8-simplex (ene) | {3,3,3,3,3,3,3} | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 0 |
| 8-cube (octo) | {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 0 |
| 8-orthoplex (ek) | {3,3,3,3,3,3,4} | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 0 |
 8-simplex |
 8-cube |
 8-orthoplex |
9 dimensions
| Name | Schläfli | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | 8-faces | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-simplex (day) | {38} | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 2 |
| 9-cube (enne) | {4,37} | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 2 |
| 9-orthoplex (vee) | {37,4} | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 2 |
 9-simplex |
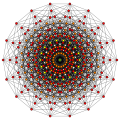 9-cube |
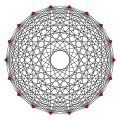 9-orthoplex |
10 dimensions
| Name | Schläfli | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | 8-faces | 9-faces | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-simplex (ux) | {39} | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 0 |
| 10-cube (deker) | {4,38} | 1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 0 |
| 10-orthoplex (ka) | {38,4} | 20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 0 |
 10-simplex |
 10-cube |
 10-orthoplex |
...
Non-convex
There are no non-convex regular polytopes in five dimensions or higher.
Tessellations of Euclidean space
Tessellations of Euclidean 4-space
There are three kinds of infinite regular tessellations (honeycombs) that can tessellate Euclidean four-dimensional space:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Tesseractic honeycomb (test) |
{4,3,3,4} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | {3,3,4} | Self-dual |
| 16-cell honeycomb (hext) |
{3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,4,3,3} |
| 24-cell honeycomb (icot) |
{3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {4,3,3} | {3,3,4,3} |
 Projected portion of {4,3,3,4} (Tesseractic honeycomb) |
 Projected portion of {3,3,4,3} (16-cell honeycomb) |
 Projected portion of {3,4,3,3} (24-cell honeycomb) |
Tessellations of Euclidean 5-space and higher
The hypercubic honeycomb is the only family of regular honeycomb that can tessellate each dimension, five or higher, formed by hypercube facets, four around every ridge.
| Name | Schläfli {p1, p2, ..., pn−1} |
Facet type |
Vertex figure |
Dual |
|---|---|---|---|---|
| Square tiling (squat) | {4,4} | {4} | {4} | Self-dual |
| Cubic honeycomb (chon) | {4,3,4} | {4,3} | {3,4} | Self-dual |
| Tesseractic honeycomb (test) | {4,32,4} | {4,32} | {32,4} | Self-dual |
| 5-cube honeycomb (penth) | {4,33,4} | {4,33} | {33,4} | Self-dual |
| 6-cube honeycomb | {4,34,4} | {4,34} | {34,4} | Self-dual |
| 7-cube honeycomb | {4,35,4} | {4,35} | {35,4} | Self-dual |
| 8-cube honeycomb | {4,36,4} | {4,36} | {36,4} | Self-dual |
| n-hypercubic honeycomb | {4,3n−2,4} | {4,3n−2} | {3n−2,4} | Self-dual |
Tessellations of hyperbolic space
Tessellations of hyperbolic 4-space
There are seven convex regular honeycombs and four star-honeycombs in H4 space.[5] Five convex ones are compact, and two are paracompact.
Five compact regular honeycombs in H4:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Order-5 5-cell honeycomb | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} |
| 120-cell honeycomb | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} |
| Order-5 tesseractic honeycomb | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} |
| Order-4 120-cell honeycomb | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} |
| Order-5 120-cell honeycomb | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Self-dual |
The two paracompact regular H4 honeycombs are: {3,4,3,4}, {4,3,4,3}.
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Order-4 24-cell honeycomb | {3,4,3,4} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {4,3,4} | {4,3,4,3} |
| Cubic honeycomb honeycomb | {4,3,4,3} | {4,3,4} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,4,3,4} |
There are four regular star-honeycombs in H4 space:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Small stellated 120-cell honeycomb | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} |
| Pentagrammic-order 600-cell honeycomb | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} |
| Order-5 icosahedral 120-cell honeycomb | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} |
| Great 120-cell honeycomb | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
Tessellations of hyperbolic 5-space
There are 5 regular honeycombs in H5, all paracompact, which include infinite (Euclidean) facets or vertex figures: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4}, and {4,3,3,4,3}.
There are no compact regular tessellations of hyperbolic space of dimension 5 or higher and no paracompact regular tessellations in hyperbolic space of dimension 6 or higher.
| Name | Schläfli Symbol {p,q,r,s,t} |
Facet type {p,q,r,s} |
4-face type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Cell figure {t} |
Face figure {s,t} |
Edge figure {r,s,t} |
Vertex figure {q,r,s,t} |
Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| 5-orthoplex honeycomb | {3,3,3,4,3} | {3,3,3,4} | {3,3,3} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,3} |
| 24-cell honeycomb honeycomb | {3,4,3,3,3} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {3,3,3} | {3,3,3,3} | {3,3,3,4,3} |
| 16-cell honeycomb honeycomb | {3,3,4,3,3} | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {3,3} | {4,3,3} | {3,4,3,3} | self-dual |
| Order-4 24-cell honeycomb honeycomb | {3,4,3,3,4} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {3,3,4} | {4,3,3,4} | {4,3,3,4,3} |
| Tesseractic honeycomb honeycomb | {4,3,3,4,3} | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,4} |
Tessellations of hyperbolic 6-space and higher
Even allowing for infinite (Euclidean) facets and/or vertex figures, there are no regular compact or paracompact tessellations of hyperbolic space of dimension 6 or higher.
Apeirotopes
An apeirotope is, like any other polytope, an unbounded hyper-surface. The difference is that whereas a polytope's hyper-surface curls back on itself to close round a finite volume of hyperspace, an apeirotope does not curl back.
Some people regard apeirotopes as just a special kind of polytope, while others regard them as rather different things.
Two dimensions
A regular apeirogon is a regular division of an infinitely long line into equal segments, joined by vertices. It has regular embeddings in the plane, and in higher-dimensional spaces. In two dimensions it can form a straight line or a zig-zag. In three dimensions, it traces out a helical spiral. The zig-zag and spiral forms are said to be skew.
Three dimensions
An apeirohedron is an infinite polyhedral surface. Like an apeirogon, it can be flat or skew. A flat apeirohedron is just a tiling of the plane. A skew apeirohedron is an intricate honeycomb-like structure which divides space into two regions.
There are thirty regular apeirohedra in Euclidean space.[6] These include the tessellations of type {4,4}, {6,3}, {3,6} above, as well as (in the plane) polytopes of type: {∞,3}, {∞,4}, {∞,6} and in 3-dimensional space, blends of these with either an apeirogon or a line segment, and the "pure" 3-dimensional apeirohedra (12 in number)
See also regular skew polyhedron.
Abstract polytopes
The abstract polytopes arose out of an attempt to study polytopes apart from the geometrical space they are embedded in. They include the tessellations of spherical, euclidean and hyperbolic space, tessellations of other manifolds, and many other objects that do not have a well-defined topology, but instead may be characterised by their "local" topology. There are infinitely many in every dimension. See this atlas for a sample. Some notable examples of abstract polytopes that do not appear elsewhere in this list are the 11-cell and the 57-cell.
See also
- Polygon
- Polyhedron
- Regular polyhedron (5 regular Platonic solids and 4 Kepler–Poinsot solids)
- 4-polytope
- regular 4-polytope (16 regular 4-polytopes, 4 convex and 10 star (Schläfli–Hess))
- Uniform 4-polytope
- Tessellation
- Regular polytope
References
- ^ Regular polytopes, p. 120
- ^ Regular polytopes, p. 124
- ^ Regular polytopes, p. 66-67
- ^ (Coxeter 1973, Table I: Regular polytopes, (iii) The three regular polytopes in n dimensions (n>=5), pp. 294–295)
- ^ Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p. 213
- ^ (McMullen & Schulte 2002, Section 7E)
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, pp. 212–213) [2] PDF
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
External links
- The Platonic Solids
- Kepler-Poinsot Polyhedra
- Regular 4d Polytope Foldouts
- Multidimensional Glossary (Look up Hexacosichoron and Hecatonicosachoron)
- Polytope Viewer
- Polytopes and optimal packing of p points in n dimensional spheres
- An atlas of small regular polytopes
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | {3[11]} | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |