RockMagnetist (talk | contribs) added section headers |
m clean up spacing around commas and other punctuation fixes, replaced: ,T → , T, ,v → , v Tag: AWB |
||
| (41 intermediate revisions by 29 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Velocity profile of wind driven current with depth}} |
|||
[[Image:Ekman spirale.svg|right|thumb|200px|Ekman spiral effect. 1. Wind 2. force from above 3. Effective direction of the current 4. Coriolis effect]] |
|||
{{merge to|Ekman layer|date=March 2024 }} |
|||
[[File:Ekman spiral.gif|thumb|The Ekman spiral occurs as a consequence of the Coriolis effect.]] The '''Ekman spiral''' is an arrangement of ocean currents: the directions of horizontal current appear to twist as the depth changes.<ref>{{Cite web |last=US Department of Commerce |first=National Oceanic and Atmospheric Administration |title=The Ekman Spiral - Currents: NOAA's National Ocean Service Education |url=https://oceanservice.noaa.gov/education/tutorial_currents/04currents4.html |access-date=2024-02-07 |website=oceanservice.noaa.gov |language=EN-US}}</ref> The oceanic wind driven Ekman spiral is the result of a force balance created by a [[shear stress]] force, [[Coriolis force]] and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the [[wind stress]] force. At the bottom of the ocean, the [[shear stress]] force is created by [[friction]] with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer [[Fridtjof Nansen]] during his [[Nansen's Fram expedition|Fram expedition]]. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer [[Vagn Walfrid Ekman]], was the first person to physically explain this process.<ref>Ekman, V. W. 1905. On the influence of the Earth's rotation on ocean currents. Arch. Math. Astron. Phys., 2, 1-52. [http://empslocal.ex.ac.uk/people/staff/gv219/classics.d/Ekman05.pdf]</ref> |
|||
== Bottom Ekman spiral == |
|||
The '''Ekman spiral''' is a structure of currents or winds near a horizontal boundary in which the flow direction rotates as one moves away from the boundary. It derives its name from the [[Sweden|Swedish]] [[oceanography|oceanographer]] [[Vagn Walfrid Ekman]]. The deflection of surface currents was first noticed by the Norwegian oceanographer [[Fridtjof Nansen]] during the [[Nansen's Fram expedition|Fram expedition]] (1893–1896) and the effect was first physically explained by [[Vagn Walfrid Ekman]].<ref>Ekman, V. W. 1905. On the influence of the Earth's rotation on ocean currents. Arch. Math. Astron. Phys., 2, 1-52. [http://empslocal.ex.ac.uk/people/staff/gv219/classics.d/Ekman05.pdf]</ref> |
|||
[[File:Bottom Ekman spiral.jpg|thumb|Two figures showing the bottom Ekman spiral. The figure on the left is the 3D Ekman spiral, the figure on the right 2D.]] |
|||
In order to derive the properties of an Ekman spiral a look is taken at a uniform, horizontal [[geostrophic]] interior flow in a homogeneous fluid. This flow will be denoted by <math>\vec{u} = (\bar{u},\bar{v})</math>, where the two components are constant because of uniformity. Another result of this property is that the horizontal gradients will equal zero. As a result, the [[continuity equation]] will yield, <math>\frac{\partial w}{\partial z} = 0</math>. Note that the concerning interior flow is horizontal, so <math>w = 0</math> at all depths, even in the boundary layers. In this case, the [[Navier-Stokes equations|Navier-Stokes momentum equations]], governing geophysical motion can now be reduced to:<ref name="GFD">{{cite book |last=Cushman-Roisin |first=Benoit |last2=Beckers |first2=Jean-Marie |title=Introduction to Geophysical Fluid Dynamics |publisher=ACADEMIC PRESS |date=2009 |url=http://www.ccpo.odu.edu/~klinck/Reprints/PDF/roisinGFD2010.pdf}}</ref> |
|||
:<math> |
|||
==Theory== |
|||
\begin{align} |
|||
The effect is a consequence of the [[Coriolis effect]] which subjects moving objects to an apparent force to the right of their direction of motion in the northern hemisphere (and to the left in the Southern Hemisphere). Thus, when a persistent wind blows over an extended area of the ocean surface in the northern hemisphere, it causes a surface current which accelerates in that direction, which then experiences a Coriolis force and acceleration to the right of the wind: the current will turn gradually to the right as it gains speed. As the flow is now somewhat right of the wind, the Coriolis force perpendicular to the flow's motion is now partly directed ''against'' the wind. Eventually, the current will reach a top speed when the force of the wind, of the Coriolis effect, and the resistant drag of the subsurface water balance, and the current will flow at a constant speed and direction as long as the wind persists. This surface current drags on the water layer below it, applying a force in its own direction of motion to that layer, repeating the process whereby that layer eventually becomes a steady current even further to the right of the wind, and so on for deeper layers of water, resulting in a continuous rotation (or spiraling) of current direction with changing depth. As depth increases, the force transmitted from the driving wind declines and thus the speed of the resultant steady current decreases, hence the tapered spiral representation in the accompanying diagram. The depth to which the Ekman spiral penetrates is determined by how far turbulent mixing can penetrate over the course of a [[Foucault pendulum|pendulum day]].<ref>{{cite web |
|||
-fv &= -\frac{1}{\rho_0}\frac{\partial p}{\partial x} + \nu_E \frac{\partial^2 u}{\partial z^2}, \\[5pt] |
|||
| title=AMS Glossary |
|||
fu &= -\frac{1}{\rho_0}\frac{\partial p}{\partial y} + \nu_E \frac{\partial^2 v}{\partial z^2}, \\[5pt] |
|||
| url=http://amsglossary.allenpress.com/glossary/search?id=pendulum-day1 |
|||
0 &= -\frac{1}{\rho_0}\frac{\partial p}{\partial z}, |
|||
| accessdate=2007-06-28}}</ref> |
|||
\end{align} |
|||
</math> |
|||
Where <math>f</math> is the [[Coriolis frequency|Coriolis parameter]], <math>\rho_0</math> the fluid [[density]] and <math>\nu_E</math> the [[Viscosity|eddy viscosity]], which are all taken as a constant here for simplicity. These parameters have a small variance on the scale of an Ekman spiral, thus this approximation will hold. A uniform flow requires a uniformly varying [[pressure gradient]]. When substituting the flow components of the interior flow, <math>u = \bar{u}</math> and <math>v = \bar{v}</math>, in the equations above, the following is obtained: |
|||
The diagram above attempts to show the forces associated with the Ekman spiral as applied to the Northern hemisphere. The force from above is in red (beginning with the wind blowing over the water surface), the Coriolis force (which is shown at right angles to the force from above when it should in fact be at right angles to the actual water flow) is in dark yellow, and the net resultant water movement is in pink, which then becomes the force from above for the layer below it, accounting for the gradual clockwise spiral motion as you move down. |
|||
:<math> |
|||
==Observation== |
|||
\begin{align} |
|||
The first documented observations of an oceanic Ekman spiral were made in the Arctic Ocean from a drifting ice floe in 1958.<ref name = "Hunkins">{{cite journal | last1 = Hunkins | first1 = K. | title = Ekman drift currents in the Arctic Ocean | journal = Deep-Sea Research | volume = 13 | pages = 607–620 | year = 1966 | doi=10.1016/0011-7471(66)90592-4|bibcode = 1966DSROA..13..607H }}</ref> More recent observations include: |
|||
-f\bar{v} &= -\frac{1}{\rho_0}\frac{\partial p}{\partial x} = \text{constant} \\[5pt] |
|||
* SCUBA diving observations during a study of upwelling water transport through a kelp forest on the west coast of South Africa in 1978 <ref>Field, J. G., C. L. Griffiths, E. A. S. Linley, P. Zoutendyk and R. Carter (1981). Wind-induced water movements in a Benguela kelp bed. Coastal Upwelling. F. A. Richards (Ed.), Washington D.C., American Geophysical Union: 507-513. {{ISBN|0-87590-250-2}}</ref> |
|||
f\bar{u} &= -\frac{1}{\rho_0}\frac{\partial p}{\partial y} = \text{constant} |
|||
* The 1980 Mixed Layer Experiment<ref name = "Davis">{{cite journal | last1 = Davis | first1 = R.E. | first2 = R. | last2 = de Szoeke | first3 = P. | last3 = Niiler. | title = Part II: Modelling the mixed layer response | journal = Deep-Sea Research | volume = 28 | pages = 1453–1475 | year = 1981 | doi = 10.1016/0198-0149(81)90092-3 | issue = 12|bibcode = 1981DSRI...28.1453D }}</ref> |
|||
\end{align} |
|||
* Within the Sargasso Sea during the 1982 Long Term Upper Ocean Study <ref name = "Price">{{cite journal | last1 = Price | first1 = J.F. | last2= Weller | first2= R.A.| last3= Schudlich|first3=R.R.| title = Wind-Driven Ocean Currents and Ekman Transport | journal = Science | volume = 238 | pages = 1534–1538 | year = 1987 |bibcode = 1987Sci...238.1534P |doi = 10.1126/science.238.4833.1534 | pmid=17784291}}</ref> |
|||
</math> |
|||
* Within the California Current during the 1993 Eastern Boundary Current experiment <ref name = "Chereskin">{{cite journal|last=Chereskin|first=T.K.|title=Direct evidence for an Ekman balance in the California Current|journal=Journal of Geophysical Research|year=1995|volume=100|pages=18261–18269|bibcode = 1995JGR...10018261C |doi = 10.1029/95JC02182 }}</ref> |
|||
* Within the Drake Passage region of the Southern Ocean <ref name = "Lenn">{{cite journal|last1=Lenn|first1=Y.-D.|last2=Chereskin|first2=T.K.|title=Observation of Ekman Currents in the Southern Ocean|journal=Journal of Physical Oceanography |year=2009|volume=39|pages=768–779|doi=10.1175/2008jpo3943.1|bibcode = 2009JPO....39..768L }}</ref><ref name = "Polton">{{cite journal|last1=Polton|first1=J.A.|last2=Lenn|first2=Y.-D.|last3=Elipot|first3=S.|last4=Chereskin|first4=T.K.|last5=Sprintall|first5=J.|title=Can Drake Passage Observations Match Ekman's Classic Theory?|journal=Journal of Physical Oceanography |year=2013|volume=43|pages=1733–1740 |doi = 10.1175/JPO-D-13-034.1 |bibcode = 2013JPO....43.1733P }}</ref> |
|||
*North of the Kerguelan Plateau during the 2008 SOFINE experiment <ref name = "Roach">{{cite journal|last1=Roach|first1=C.J.|last2=Phillips|first2=H.E.|last3=Bindoff|first3=N.L.|last4=Rintoul|first4=S.R.|title=Detecting and Characterizing Ekman Currents in the Southern Ocean|journal=Journal of Physical Oceanography |year=2015|volume=45|pages=1205–1223|doi=10.1175/JPO-D-14-0115.1|bibcode = 2015JPO....45.1205R }}</ref> |
|||
Common to several of these observations spirals were found to be 'compressed', displaying larger estimates of eddy viscosity when considering the rate of rotation with depth than the eddy viscosity derived from considering the rate of decay of speed.<ref name = "Price" /><ref name = "Chereskin" /><ref name = "Lenn" /> Though in the Southern Ocean the 'compression', or spiral flattening effect disappeared when new data permitted a more careful treatment of the effect of geostrophic shear.<ref name = "Polton" /><ref name = "Roach"/> |
|||
Using the last of the three equations at the top of this section, yields that the pressure is independent of depth. |
|||
The classic Ekman spiral has been observed under sea ice,<ref name = "Hunkins" /> but observations remain rare in open-ocean conditions. This is due both to the fact that the turbulent mixing in the [[surface layer]] of the ocean has a strong [[diurnal cycle]] and to the fact that surface waves can destabilize the Ekman spiral. Ekman spirals are also found in the atmosphere. Surface winds in the Northern Hemisphere tend to blow to the left of winds aloft. |
|||
:<math> |
|||
==See also== |
|||
\begin{align} |
|||
* [[Ekman transport]] |
|||
-f(v - \bar{v}) &= \nu_E \frac{\partial^2 u}{\partial z^2} \\[5pt] |
|||
* [[Ekman layer]] |
|||
f(u - \bar{u}) &= \nu_E \frac{\partial^2 v}{\partial z^2} |
|||
* [[Secondary flow]] |
|||
\end{align} |
|||
* [[Upwelling]] |
|||
</math> |
|||
<math>u = \bar{u} + A e^{\lambda z}</math> and <math>v = \bar{v} + B e^{\lambda z}</math> will suffice as a solution to the differential equations above. After substitution of these possible solutions in the same equations, <math>\nu_E^2\lambda^4 + f^2 = 0</math> will follow. Now, <math>\lambda</math> has the following possible outcomes: |
|||
==Notes== |
|||
{{reflist}} |
|||
:<math> |
|||
==References== |
|||
\lambda = \pm (1 \pm i)\sqrt{\frac{f}{2\nu_E}} |
|||
{{Commons|Ekman spiral}} |
|||
</math> |
|||
* [http://amsglossary.allenpress.com/glossary/search?id=ekman-spiral1 AMS Glossary, mathematical description] |
|||
* A. Gnanadesikan and R.A. Weller, 1995 · "Structure and instability of the Ekman spiral in the presence of surface gravity waves" · ''Journal of Physical Oceanography'' 25(12), pp. 3148–3171. |
|||
* J.F. Price, R.A. Weller and R. Pinkel, 1986 · "Diurnal cycling: Observations and models of the upper ocean response to diurnal heating, cooling and wind mixing" · ''Journal of Geophysical Research'' 91, pp. 8411–8427. |
|||
* J.G. Richman, R. deSzoeke and R.E. Davis, 1987 · "Measurements of near-surface shear in the ocean" · ''Journal of Geophysical Research'' 92, pp. 2851–2858. |
|||
* Field, J. G., C. L. Griffiths, E. A. S. Linley, P. Zoutendyk and R. Carter, 1981 Wind-induced water movements in a Benguela kelp bed. Coastal Upwelling. F. A. Richards (Ed.), Washington D.C., American Geophysical Union: 507-513. {{ISBN|0-87590-250-2}} |
|||
Because of the [[no-slip condition]] at the bottom and the constant interior flow for <math>z \gg d</math>, coefficients <math>A</math> and <math>B</math> can be determined. In the end, this will lead to the following solution for <math>\vec{u}(z)</math>:<ref name="GFD" /> |
|||
{{physical oceanography}} |
|||
:<math> |
|||
\begin{align} |
|||
u & = \bar{u}\left[1 - e^{-z/d}\cos\left(\frac{z}{d}\right)\right] - \bar{v}e^{-z/d}\sin\left(\frac{z}{d}\right), \\[5pt] |
|||
v & = \bar{u} e^{-z/d}\sin\left(\frac{z}{d}\right) + \bar{v}\left[1 - e^{-z/d}\cos\left(\frac{z}{d}\right)\right], |
|||
\end{align} |
|||
</math> |
|||
Here, <math>d=\sqrt{\frac{2\nu_E}{f}}</math>. Note that the [[Velocity|velocity vector]] will approach the values of the interior flow, when the <math>z</math> takes the order of <math>d</math>. This is the reason why <math>d</math> is defined as the thickness of the Ekman layer. A number of important properties of the Ekman spiral will follow from this solution: |
|||
*When <math>z\rightarrow{0}</math>, it appears that the flow has a transverse component with respect to the interior flow, which differs 45 degrees to the left on the [[northern hemisphere]], <math>f>0</math>, and 45 degrees to the right on the [[southern hemisphere]], <math>f<0</math>. Note that, in this case, the angle between this flow and the interior flow is at its maximum. It will decrease for increasing <math>z</math>. |
|||
*When <math>\frac{z}{d}</math> takes the value of <math>\pi</math>, the resulting flow is in line with the interior flow, but will be increased with <math>e^{-\pi}</math>, with respect to the interior flow. |
|||
*For higher values of <math>\frac{z}{d}</math>, there will be a minimal transverse component in the other direction as before. The exponential term will go to zero for <math>z\gg d</math>, resulting in <math>\vec{u}=(\bar{u},\bar{v})</math>. Because of these properties, the velocity vector of the flow as a function of depth will look like a spiral. |
|||
== Surface Ekman spiral == |
|||
[[File:Surface Ekman spiral.jpg|thumb|Two figures showing the bottom Ekman spiral. The figure on the left is the 3D Ekman spiral, the figure on the right 2D.]] |
|||
The solution for the flow forming the bottom Ekman spiral was a result of the [[shear stress]] exerted on the flow by the bottom. Logically, wherever [[shear stress]] can be exerted on a flow, Ekman spirals will form. This is the case at the air–water interface, because of wind. A situation is considered where a [[wind stress]] <math>\vec{\tau} = (\tau_x,\tau_y)</math> is exerted along a water-surface with an interior flow <math>\vec{u} = (u,v)</math> beneath. Again, the flow is uniform, has a geostrophic interior and is homogeneous fluid. The equations of motion for a geostrophic flow, which are the same as stated in the bottom spiral section, can be reduced to:<ref name="GFD" /> |
|||
:<math> |
|||
\begin{align} |
|||
-f(v - \bar{v}) &= \nu_E \frac{\partial^2 u}{\partial z^2} \\[5pt] |
|||
f(u - \bar{u}) &= \nu_E \frac{\partial^2 v}{\partial z^2} \\ |
|||
\end{align} |
|||
</math> |
|||
The boundary conditions for this case are as follows: |
|||
* Surface <math>(z = 0)</math>: <math>\;\;\;\rho_0\nu_E\frac{\partial u}{\partial z} = \tau_x\;</math> and <math>\;\rho_0\nu_E\frac{\partial v}{\partial z}=\tau_y</math> |
|||
* Towards interior <math>(z \rightarrow{-\infty})</math>: <math>\;\;\;u=\bar{u}\;</math> and <math>\;v = \bar{v}</math> |
|||
With these conditions, the solution can be determined:<ref name="GFD" /> |
|||
:<math> |
|||
\begin{align} |
|||
u & = \bar{u} + \frac{\sqrt{2}}{\rho_0 fd}e^{z/d}\left[\tau_x \cos\left(\frac{z}{d} - \frac{\pi}{4}\right) - \tau_y \sin\left(\frac{z}{d} - \frac{\pi}{4}\right)\right] \\[5pt] |
|||
v & = \bar{v} + \frac{\sqrt{2}}{\rho_0 fd}e^{z/d}\left[\tau_x \sin\left(\frac{z}{d} - \frac{\pi}{4}\right) + \tau_y \cos\left(\frac{z}{d} - \frac{\pi}{4}\right)\right] |
|||
\end{align} |
|||
</math> |
|||
Some differences with respect to the bottom Ekman spiral emerge. The deviation from the interior flow is exclusively dependent on the [[wind stress]] and not on the interior flow. Whereas in the case of the bottom Ekman spiral, the deviation is determined by the interior flow. The wind-driven component of the flow is inversely proportional with respect to the Ekman-layer thickness <math>d</math>. So if the layer thickness is small, because of a small viscosity of the fluid for example, this component could be very large. At last, the flow at the surface is 45 degrees to the right on the [[northern hemisphere]] and 45 degrees to the left on the [[southern hemisphere]] with respect to the wind-direction. In case of the bottom Ekman spiral, this is the other way around. |
|||
== Observations == |
|||
The equations and assumptions above are not representative for the actual observations of the Ekman spiral. The differences between the theory and the observations are that the angle is between 5–20 degrees instead of the 45 degrees as expected<ref>Stacey, M. W., S. Pond, and P. H. LeBlond, 1986: A wind-forced Ekman spiral as a good statistical fit to low-frequency currents in coastal strait. Science, 233, 470–472</ref> and that the Ekman layer depth and thus the Ekman spiral is less deep than expected. There are three main factors which contribute to the reason why this is, [[Stratification (water)|stratification]],<ref>Price, J. F., and M. A. Sundermeyer, 1999: Stratified Ekman layers. J. Geophys. Res., 104, 20467–20494.</ref> [[turbulence]] and horizontal gradients.<ref name="GFD" /> Other less important factors which play a role in this are the [[Stokes drift]],<ref>van den Bremer TS, BreivikØ. 2017 Stokes drift.Phil.Trans.R.Soc.A376:20170104.http://dx.doi.org/10.1098/rsta.2017.0104</ref> [[wave]]s and the [[Coriolis-Stokes force|Stokes-Coriolis force]].<ref>Jeff A. Polton, David M. Lewis, and Stephen E. Belcher, 01 Apr 2005: The Role of Wave-Induced Coriolis–Stokes Forcing on the Wind-Driven Mixed Layer. Journal of Physical Oceanography, Volume 35: Issue 4, 444–457</ref> |
|||
== References == |
|||
{{Reflist}}{{Physical oceanography}} |
|||
[[Category:Oceanography]] |
[[Category:Oceanography]] |
||
Latest revision as of 16:49, 27 March 2024
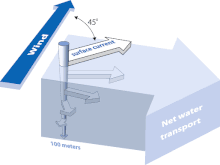
The Ekman spiral is an arrangement of ocean currents: the directions of horizontal current appear to twist as the depth changes.[1] The oceanic wind driven Ekman spiral is the result of a force balance created by a shear stress force, Coriolis force and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the wind stress force. At the bottom of the ocean, the shear stress force is created by friction with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer Fridtjof Nansen during his Fram expedition. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer Vagn Walfrid Ekman, was the first person to physically explain this process.[2]
Bottom Ekman spiral[edit]

In order to derive the properties of an Ekman spiral a look is taken at a uniform, horizontal geostrophic interior flow in a homogeneous fluid. This flow will be denoted by , where the two components are constant because of uniformity. Another result of this property is that the horizontal gradients will equal zero. As a result, the continuity equation will yield, . Note that the concerning interior flow is horizontal, so at all depths, even in the boundary layers. In this case, the Navier-Stokes momentum equations, governing geophysical motion can now be reduced to:[3]
Where is the Coriolis parameter, the fluid density and the eddy viscosity, which are all taken as a constant here for simplicity. These parameters have a small variance on the scale of an Ekman spiral, thus this approximation will hold. A uniform flow requires a uniformly varying pressure gradient. When substituting the flow components of the interior flow, and , in the equations above, the following is obtained:
Using the last of the three equations at the top of this section, yields that the pressure is independent of depth.
and will suffice as a solution to the differential equations above. After substitution of these possible solutions in the same equations, will follow. Now, has the following possible outcomes:
Because of the no-slip condition at the bottom and the constant interior flow for , coefficients and can be determined. In the end, this will lead to the following solution for :[3]
Here, . Note that the velocity vector will approach the values of the interior flow, when the takes the order of . This is the reason why is defined as the thickness of the Ekman layer. A number of important properties of the Ekman spiral will follow from this solution:
- When , it appears that the flow has a transverse component with respect to the interior flow, which differs 45 degrees to the left on the northern hemisphere, , and 45 degrees to the right on the southern hemisphere, . Note that, in this case, the angle between this flow and the interior flow is at its maximum. It will decrease for increasing .
- When takes the value of , the resulting flow is in line with the interior flow, but will be increased with , with respect to the interior flow.
- For higher values of , there will be a minimal transverse component in the other direction as before. The exponential term will go to zero for , resulting in . Because of these properties, the velocity vector of the flow as a function of depth will look like a spiral.
Surface Ekman spiral[edit]

The solution for the flow forming the bottom Ekman spiral was a result of the shear stress exerted on the flow by the bottom. Logically, wherever shear stress can be exerted on a flow, Ekman spirals will form. This is the case at the air–water interface, because of wind. A situation is considered where a wind stress is exerted along a water-surface with an interior flow beneath. Again, the flow is uniform, has a geostrophic interior and is homogeneous fluid. The equations of motion for a geostrophic flow, which are the same as stated in the bottom spiral section, can be reduced to:[3]
The boundary conditions for this case are as follows:
- Surface : and
- Towards interior : and
With these conditions, the solution can be determined:[3]
Some differences with respect to the bottom Ekman spiral emerge. The deviation from the interior flow is exclusively dependent on the wind stress and not on the interior flow. Whereas in the case of the bottom Ekman spiral, the deviation is determined by the interior flow. The wind-driven component of the flow is inversely proportional with respect to the Ekman-layer thickness . So if the layer thickness is small, because of a small viscosity of the fluid for example, this component could be very large. At last, the flow at the surface is 45 degrees to the right on the northern hemisphere and 45 degrees to the left on the southern hemisphere with respect to the wind-direction. In case of the bottom Ekman spiral, this is the other way around.
Observations[edit]
The equations and assumptions above are not representative for the actual observations of the Ekman spiral. The differences between the theory and the observations are that the angle is between 5–20 degrees instead of the 45 degrees as expected[4] and that the Ekman layer depth and thus the Ekman spiral is less deep than expected. There are three main factors which contribute to the reason why this is, stratification,[5] turbulence and horizontal gradients.[3] Other less important factors which play a role in this are the Stokes drift,[6] waves and the Stokes-Coriolis force.[7]
References[edit]
- ^ US Department of Commerce, National Oceanic and Atmospheric Administration. "The Ekman Spiral - Currents: NOAA's National Ocean Service Education". oceanservice.noaa.gov. Retrieved 2024-02-07.
- ^ Ekman, V. W. 1905. On the influence of the Earth's rotation on ocean currents. Arch. Math. Astron. Phys., 2, 1-52. [1]
- ^ a b c d e Cushman-Roisin, Benoit; Beckers, Jean-Marie (2009). Introduction to Geophysical Fluid Dynamics (PDF). ACADEMIC PRESS.
- ^ Stacey, M. W., S. Pond, and P. H. LeBlond, 1986: A wind-forced Ekman spiral as a good statistical fit to low-frequency currents in coastal strait. Science, 233, 470–472
- ^ Price, J. F., and M. A. Sundermeyer, 1999: Stratified Ekman layers. J. Geophys. Res., 104, 20467–20494.
- ^ van den Bremer TS, BreivikØ. 2017 Stokes drift.Phil.Trans.R.Soc.A376:20170104.http://dx.doi.org/10.1098/rsta.2017.0104
- ^ Jeff A. Polton, David M. Lewis, and Stephen E. Belcher, 01 Apr 2005: The Role of Wave-Induced Coriolis–Stokes Forcing on the Wind-Driven Mixed Layer. Journal of Physical Oceanography, Volume 35: Issue 4, 444–457



![{\displaystyle {\begin{aligned}-fv&=-{\frac {1}{\rho _{0}}}{\frac {\partial p}{\partial x}}+\nu _{E}{\frac {\partial ^{2}u}{\partial z^{2}}},\\[5pt]fu&=-{\frac {1}{\rho _{0}}}{\frac {\partial p}{\partial y}}+\nu _{E}{\frac {\partial ^{2}v}{\partial z^{2}}},\\[5pt]0&=-{\frac {1}{\rho _{0}}}{\frac {\partial p}{\partial z}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22744eef420a27bceb685bff3a3c46c8ef7ea0c7)





![{\displaystyle {\begin{aligned}-f{\bar {v}}&=-{\frac {1}{\rho _{0}}}{\frac {\partial p}{\partial x}}={\text{constant}}\\[5pt]f{\bar {u}}&=-{\frac {1}{\rho _{0}}}{\frac {\partial p}{\partial y}}={\text{constant}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e95893564ae14174d814635122e5fbc4187a437)
![{\displaystyle {\begin{aligned}-f(v-{\bar {v}})&=\nu _{E}{\frac {\partial ^{2}u}{\partial z^{2}}}\\[5pt]f(u-{\bar {u}})&=\nu _{E}{\frac {\partial ^{2}v}{\partial z^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d0ef435f3fe313654442f2e6bf24d54120caa2a)









![{\displaystyle {\begin{aligned}u&={\bar {u}}\left[1-e^{-z/d}\cos \left({\frac {z}{d}}\right)\right]-{\bar {v}}e^{-z/d}\sin \left({\frac {z}{d}}\right),\\[5pt]v&={\bar {u}}e^{-z/d}\sin \left({\frac {z}{d}}\right)+{\bar {v}}\left[1-e^{-z/d}\cos \left({\frac {z}{d}}\right)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84428d0a34c0d4ce43e6fd49a44c096214cc93b9)











![{\displaystyle {\begin{aligned}-f(v-{\bar {v}})&=\nu _{E}{\frac {\partial ^{2}u}{\partial z^{2}}}\\[5pt]f(u-{\bar {u}})&=\nu _{E}{\frac {\partial ^{2}v}{\partial z^{2}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9e55a73154679fb972615030af15430cbcafc10)






![{\displaystyle {\begin{aligned}u&={\bar {u}}+{\frac {\sqrt {2}}{\rho _{0}fd}}e^{z/d}\left[\tau _{x}\cos \left({\frac {z}{d}}-{\frac {\pi }{4}}\right)-\tau _{y}\sin \left({\frac {z}{d}}-{\frac {\pi }{4}}\right)\right]\\[5pt]v&={\bar {v}}+{\frac {\sqrt {2}}{\rho _{0}fd}}e^{z/d}\left[\tau _{x}\sin \left({\frac {z}{d}}-{\frac {\pi }{4}}\right)+\tau _{y}\cos \left({\frac {z}{d}}-{\frac {\pi }{4}}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1615085667d0c8dcd4f205c632ea5cfe770626d)

