THC Science

The Fibonacci sequence is constant-recursive: each element of the sequence is the sum of the previous two.

Hasse diagram of some subsets of constant-recursive sequences, ordered by inclusion

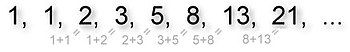
In mathematics and theoretical computer science, a constant-recursive sequence or linear recurrence sequence is an infinite sequence of numbers in which each number in the sequence is equal to a linear combination of one or more of its immediate predecessors.

The most famous example of a constant-recursive sequence is the Fibonacci sequence, in which each number is the sum of the previous two; formally, we say that it satisfies the linear recurrence relation $F(n)=F(n-1)+F(n-2)$ , where $F(n)$ is the $n$ th Fibonacci number. Generalizing this idea, a constant-recursive sequence $s(n)$ satisfies a formula of the form

s(n)=c_{1}s(n-1)+c_{2}s(n-2)+\dots +c_{d}s(n-d),

where $c_{i}$ are constants. In addition to the Fibonacci sequence, constant-recursive sequences include many other well-known sequences, such as arithmetic progressions, geometric progressions, and polynomials.

Constant-recursive sequences arise in combinatorics and the theory of finite differences; in algebraic number theory, due to the relation of the sequence to the roots of a polynomial; in the analysis of algorithms in the running time of simple recursive functions; and in formal language theory, where they count strings up to a given length in a regular language. Constant-recursive sequences are closed under important mathematical operations such as pointwise addition, pointwise multiplication, and Cauchy product. A seminal result is the Skolem–Mahler–Lech theorem, which states that the zeros of a constant-recursive sequence have a regularly repeating (eventually periodic) form. On the other hand, the Skolem problem, which asks for algorithm to determine whether a linear recurrence has at least one zero, remains one of the unsolved problems in mathematics.

Definition

An order-d homogeneous linear recurrence relation is an equation of the form

s(n)=c_{1}s(n-1)+c_{2}s(n-2)+\dots +c_{d}s(n-d),

where the d coefficients $c_{1},c_{2},\dots ,c_{d}$ are coefficients ranging over the integers, rational numbers, algebraic numbers, real numbers, or complex numbers.

A sequence $s(0),s(1),s(2),\dots$ (ranging over the same domain as the coefficients) is a constant-recursive sequence if there is an order-d homogeneous linear recurrence with constant coefficients that it satisfies for all $n\geq d$ . Note that this definition allows eventually-periodic sequences such as $1,0,0,0,\ldots$ and $0,1,0,0,\ldots$ , which are disallowed by some authors.^[1] These sequences can be excluded by requiring that $c_{d}\neq 0$ .

The order of a constant-recursive sequence is the smallest $d\geq 1$ such that the sequence satisfies an order-d homogeneous linear recurrence, or $d=0$ for the everywhere-zero sequence.

Equivalent definitions

In terms of vector spaces

A sequence $s(n)_{n\geq 0}$ is constant-recursive if and only if the set of sequences

\{s(n+r)_{n\geq 0}:r\geq 0\}

is contained in a vector space whose dimension is finite, i.e. a finite-dimensional subspace of $\mathbb {C} ^{\mathbb {N} }$ closed under the left-shift operator. This is because the order- $d$ linear recurrence relation can be understood as a proof of linear dependence between the vectors $s(n+r)_{n\geq 0}$ for $r=0,\ldots ,d$ . An extension of this argument shows that the order of the sequence is equal to the dimension of the vector space generated by $s(n+r)_{n\geq 0}$ for all $r$ .

In terms of non-homogeneous linear recurrences

A non-homogeneous linear recurrence is an equation of the form

s(n)=c_{1}s(n-1)+c_{2}s(n-2)+\dots +c_{d}s(n-d)+c

where $c$ is an additional constant. Any sequence satisfying a non-homogeneous linear recurrence is constant-recursive. This is because subtracting the equation for $s(n-1)$ from the equation for $s(n)$ yields a homogeneous recurrence for $s(n)-s(n-1)$ , from which we can solve for $s(n)$ to obtain

s(n)=(c_{1}+1)s(n-1)+(c_{2}-c_{1})s(n-2)+\dots +(c_{d}-c_{d-1})s(n-d)-c_{d}s(n-d-1).

Examples

Fibonacci sequence

The sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... of Fibonacci numbers is constant-recursive of order 2 because it satisfies the recurrence $F(n)=F(n-1)+F(n-2)$ with $F(0)=0,F(1)=1$ . For example, $F(2)=F(1)+F(0)=1+0=1$ and $F(6)=F(5)+F(4)=5+3=8$ .

Lucas sequences

The sequence 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, ... (sequence A000032 in the OEIS) of Lucas numbers satisfies the same recurrence as the Fibonacci sequence but with initial conditions $L(0)=2$ and $L(1)+1$ . More generally, every Lucas sequence is constant-recursive of order 2.

Arithmetic progressions

For any $a$ and any $r\neq 0$ , the arithmetic progression $a,a+r,a+2r,\ldots$ is constant-recursive of order 2, because it satisfies $s(n)=2s(n-1)-s(n-2)$ . Generalizing this, see polynomial sequences below.

Geometric progressions

For any $a\neq 0$ and $r$ , the geometric progression $a,ar,ar^{2},\ldots$ is constant-recursive of order 1, because it satisfies $s(n)=rs(n-1)$ . This includes, for example, the sequence 1, 2, 4, 8, 16, ... as well as the rational number sequence $1,{\frac {1}{2}},{\frac {1}{4}},{\frac {1}{8}},{\frac {1}{16}},...$ .

Eventually periodic sequences

A sequence that is eventually periodic with period length $\ell$ is constant-recursive, since it satisfies $s(n)=s(n-\ell )$ for all $n\geq d$ , where the order $d$ is the length of the initial segment including the first repeating block. Examples of such sequences are 1, 0, 0, 0, ... (order 1) and 1, 6, 6, 6, ... (order 2).

Polynomial sequences

For any polynomial $s(n)$ , the sequence of its values is a constant-recursive sequence. If the degree of the polynomial is $d$ , the sequence satisfies a recurrence of order $d+1$ , with coefficients given by the corresponding element of the binomial transform.^[2] The first few such equations are

s(n)=1\cdot s(n-1)

for a degree 0 (that is, constant) polynomial,

s(n)=2\cdot s(n-1)-1\cdot s(n-2)

for a degree 1 or less polynomial,

s(n)=3\cdot s(n-1)-3\cdot s(n-2)+1\cdot s(n-3)

for a degree 2 or less polynomial, and

s(n)=4\cdot s(n-1)-6\cdot s(n-2)+4\cdot s(n-3)-1\cdot s(n-4)

for a degree 3 or less polynomial.

A sequence obeying the order-d equation also obeys all higher order equations. These identities may be proved in a number of ways, including via the theory of finite differences.^{[citation needed]} Any sequence of $d+1$ integer, real, or complex values can be used as initial conditions for a constant-recursive sequence of order $d+1$ . If the initial conditions lie on a polynomial of degree $d-1$ or less, then the constant-recursive sequence also obeys a lower order equation.

Enumeration of words in a regular language

Let $L$ be a regular language, and let $s(n)$ be the number of words of length $n$ in $L$ . Then $s(n)_{n\geq 0}$ is constant-recursive. For example, $s(n)=2^{n}$ for the language of all binary strings, $s(n)=1$ for the language of all unary strings, and $s(n)=F(n+2)$ for the language of all binary strings that do not have two consecutive ones. More generally, any function accepted by a weighted automaton over the unary alphabet $\Sigma =\{a\}$ over the semiring $(\mathbb {R} ,+,\times )$ is constant-recursive.

Other examples

The sequences of Jacobsthal numbers, Padovan numbers, Pell numbers, and Perrin numbers are constant-recursive.

Closed-form characterizations

In terms of exponential polynomials

The characteristic polynomial (or "auxiliary polynomial") of the recurrence is the polynomial

x^{d}-c_{1}x^{d-1}-\dots -c_{d-1}x-c_{d}

whose coefficients are the same as those of the recurrence. If $c_{d}\neq 0$ , the nth term $s(n)$ of a constant-recursive sequence can be written in terms of the roots of its characteristic polynomial. If the d roots $r_{1},r_{2},\dots ,r_{d}$ are all distinct, then the nth term of the sequence is

s(n)=k_{1}r_{1}^{n}+k_{2}r_{2}^{n}+\dots +k_{d}r_{d}^{n}

where the coefficients k_i are constants that can be determined from the initial conditions.

For the Fibonacci sequence, the characteristic polynomial is $x^{2}-x-1$ , whose roots $\phi ={\frac {1+{\sqrt {5}}}{2}}$ and ${\bar {\phi }}={\frac {1-{\sqrt {5}}}{2}}$ appear in Binet's formula

F_{n}={\frac {\phi ^{n}-{\bar {\phi }}^{n}}{\sqrt {5}}}.

More generally, if a root r of the characteristic polynomial has multiplicity m, then the term $r^{n}$ is multiplied by a degree- $(m-1)$ polynomial in n. That is, let $r_{1},\dots ,r_{e}$ be the distinct roots of the characteristic polynomial. Then

s(n)=k_{1}(n)r_{1}^{n}+k_{2}(n)r_{2}^{n}+\dots +k_{e}(n)r_{e}^{n}

where $k_{i}(n)$ is a polynomial of degree $m_{i}-1$ . For instance, if the characteristic polynomial factors as $(x-r)^{3}$ , with the same root r occurring three times, then the nth term is of the form

s(n)=(a+bn+cn^{2})r^{n}.

^[3]

Conversely, if there are polynomials $k_{i}(n)$ such that

s(n)=k_{1}(n)r_{1}^{n}+k_{2}(n)r_{2}^{n}+\dots +k_{e}(n)r_{e}^{n},

then $s(n)_{n\geq 0}$ is constant-recursive.

In terms of rational generating functions

A sequence is constant-recursive precisely when its generating function

\sum _{n\geq 0}s(n)x^{n}=s(0)+s(1)x^{1}+s(2)x^{2}+s(3)x^{3}+\cdots

is a rational function. The denominator is the polynomial obtained from the auxiliary polynomial by reversing the order of the coefficients, and the numerator is determined by the initial values of the sequence.^[4]

The generating function of the Fibonacci sequence is

{\frac {x}{1-x-x^{2}}}.

In general, multiplying a generating function by the polynomial

1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}

yields a series

\left(s(0)+s(1)x^{1}+s(2)x^{2}+\cdots \right)\left(1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}\right)=\left(b_{0}+b_{1}x^{1}+b_{2}x^{2}+\cdots \right),

where

b_{n}=s(n)-c_{1}s(n-1)-c_{2}s(n-2)-\dots -c_{d}s(n-d).

If $s(n)$ satisfies the recurrence relation

s(n)=c_{1}s(n-1)+c_{2}s(n-2)+\dots +c_{d}s(n-d),

then $b_{n}=0$ for all $n\geq d$ . In other words,

\left(s(0)+s(1)x^{1}+s(2)x^{2}+\cdots \right)\left(1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}\right)=\left(b_{0}+b_{1}x^{1}+b_{2}x^{2}+\dots +b_{d-1}x^{d-1}\right),

so we obtain the rational function

\sum _{n\geq 0}s(n)x^{n}={\frac {b_{0}+b_{1}x^{1}+b_{2}x^{2}+\dots +b_{d-1}x^{d-1}}{1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}}}.

In the special case of a periodic sequence satisfying $s(n)=s(n-d)$ for $n\geq d$ , the generating function is

{\begin{aligned}{\frac {s(0)+s(1)x^{1}+\dots +s(d-1)x^{d-1}}{1-x^{d}}}=&\left(s(0)+s(1)x^{1}+\dots +s(d-1)x^{d-1}\right)+\left(s(0)+s(1)x^{1}+\dots +s(d-1)x^{d-1}\right)x^{d}+{}\\&\left(s(0)+s(1)x^{1}+\dots +s(d-1)x^{d-1}\right)x^{2d}+\cdots \end{aligned}}

by expanding the geometric series.

The generating function of the Catalan numbers is not a rational function, which implies that the Catalan numbers do not satisfy a linear recurrence with constant coefficients.

Closure properties

The termwise addition or multiplication of two constant-recursive sequences is again constant-recursive. This follows from the characterization in terms of exponential polynomials.

The Cauchy product of two constant-recursive sequences is constant-recursive. This follows from the characterization in terms of rational generating functions.

Generalizations

A natural generalization is obtained by relaxing the condition that the coefficients of the recurrence are constants. If the coefficients are allowed to be polynomials, then one obtains holonomic sequences.

A $k$ -regular sequence satisfies linear recurrences with constant coefficients, but the recurrences take a different form. Rather than $s(n)$ being a linear combination of $s(m)$ for some integers $m$ that are close to $n$ , each term $s(n)$ in a $k$ -regular sequence is a linear combination of $s(m)$ for some integers $m$ whose base- $k$ representations are close to that of $n$ . Constant-recursive sequences can be thought of as $1$ -regular sequences, where the base-1 representation of $n$ consists of $n$ copies of the digit $1$ .

Notes

^ Kauers, Manuel; Paule, Peter (2010-12-01). The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates. Springer Vienna. ISBN 978-3-7091-0444-6.
^ Boyadzhiev, Boyad (2012). "Close Encounters with the Stirling Numbers of the Second Kind" (PDF). Math. Mag. 85: 252–266.
^ Greene, Daniel H.; Knuth, Donald E. (1982), "2.1.1 Constant coefficients – A) Homogeneous equations", Mathematics for the Analysis of Algorithms (2nd ed.), Birkhäuser, p. 17.
^ Martino, Ivan; Martino, Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum. 88 (3): 569–574. arXiv:1207.0111. doi:10.1007/s00233-013-9551-2. ISSN 0037-1912.

References

Brousseau, Alfred (1971). Linear Recursion and Fibonacci Sequences. Fibonacci Association.
Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Concrete Mathematics: A Foundation for Computer Science (2 ed.). Addison-Wesley. ISBN 978-0-201-55802-9.

External links

"OEIS Index Rec". OEIS index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients)

[1] Kauers, Manuel; Paule, Peter (2010-12-01). The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates. Springer Vienna. ISBN 978-3-7091-0444-6.

[2] Boyadzhiev, Boyad (2012). "Close Encounters with the Stirling Numbers of the Second Kind" (PDF). Math. Mag. 85: 252–266.

[3] Greene, Daniel H.; Knuth, Donald E. (1982), "2.1.1 Constant coefficients – A) Homogeneous equations", Mathematics for the Analysis of Algorithms (2nd ed.), Birkhäuser, p. 17.

[4] Martino, Ivan; Martino, Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum. 88 (3): 569–574. arXiv:1207.0111. doi:10.1007/s00233-013-9551-2. ISSN 0037-1912.

[1]

[2]

[3]

[4]

@@ Line 11: / Line 11: @@
 where <math>c_i</math> are [[Constant (mathematics)|constant]]s. In addition to the Fibonacci sequence, constant-recursive sequences include many other well-known sequences, such as [[arithmetic progression]]s, [[geometric progression]]s, and [[polynomial]]s.
-Constant-recursive sequences arise in [[combinatorics]] and the theory of [[finite difference]]s; in [[algebraic number theory]], due to the relation of the sequence to the roots of a polynomial; in the [[analysis of algorithms]] in the running time of simple [[Recursion (computer science)|recursive function]]s; and in [[formal language theory]], where they count the number of strings up to a given length in a [[regular language]]. Constant-recursive sequences are closed under important mathematical operations such as [[pointwise]] [[addition]], pointwise [[multiplication]], and [[Cauchy product]]. A seminal result is the [[Skolem–Mahler–Lech theorem]], which states that the [[Zero of a function|zeros]] of a constant-recursive sequence have a regularly repeating (eventually periodic) form. On the other hand, the [[Skolem problem]], which asks for [[algorithm]] to determine whether a linear recurrence has at least one zero, remains one of the [[List of unsolved problems in mathematics|unsolved problems in mathematics]].
+Constant-recursive sequences arise in [[combinatorics]] and the theory of [[finite difference]]s; in [[algebraic number theory]], due to the relation of the sequence to the roots of a polynomial; in the [[analysis of algorithms]] in the running time of simple [[Recursion (computer science)|recursive function]]s; and in [[formal language theory]], where they count strings up to a given length in a [[regular language]]. Constant-recursive sequences are closed under important mathematical operations such as [[pointwise]] [[addition]], pointwise [[multiplication]], and [[Cauchy product]]. A seminal result is the [[Skolem–Mahler–Lech theorem]], which states that the [[Zero of a function|zeros]] of a constant-recursive sequence have a regularly repeating (eventually periodic) form. On the other hand, the [[Skolem problem]], which asks for [[algorithm]] to determine whether a linear recurrence has at least one zero, remains one of the [[List of unsolved problems in mathematics|unsolved problems in mathematics]].
 ==Definition==