Eric Rowland (talk | contribs) eventually periodic sequences |
Caleb Stanford (talk | contribs) inline math Tag: 2017 wikitext editor |
||
| (220 intermediate revisions by 27 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Infinite sequence of numbers satisfying a linear equation}} |
|||
{{AFC submission|t||ts=20160309180423|u=Eric Rowland|ns=118|demo=}} <!--- Important, do not remove this line before article has been created. ---> |
|||
[[File:Fibonacci sequence.jpg|thumb|350px|right|The Fibonacci sequence is constant-recursive: each element of the sequence is the sum of the previous two.]] |
|||
[[File:Constant-recursive-sequences.svg|thumb|350px|right|[[Hasse diagram]] of some subclasses of constant-recursive sequences, ordered by inclusion]] |
|||
In [[mathematics]], an [[sequence|infinite sequence]] of [[number]]s <math>s_0, s_1, s_2, s_3, \ldots</math> is called '''constant-recursive''' if it satisfies an equation of the form |
|||
==Examples== |
|||
:<math display=block>s_n = c_1 s_{n-1} + c_2 s_{n-2} + \dots + c_d s_{n-d},</math> |
|||
for all <math>n \ge d</math>, where <math>c_i</math> are [[constant (mathematics)|constant]]s. The equation is called a [[linear recurrence with constant coefficients|linear recurrence relation]]. |
|||
The concept is also known as a '''linear recurrence sequence''', '''linear-recursive sequence''', '''linear-recurrent sequence''', or a '''C-finite sequence'''.{{sfn|Kauers|Paule|2010|p=63}} |
|||
For example, the [[Fibonacci sequence]] |
|||
:<math>0, 1, 1, 2, 3, 5, 8, 13, \ldots</math>, |
|||
The sequence of [[Fibonacci number]]s satisfies the recurrence |
|||
is constant-recursive because it satisfies the linear recurrence <math>F_n = F_{n-1} + F_{n-2}</math>: each number in the sequence is the sum of the previous two.{{sfn|Kauers|Paule|2010|p=70}} |
|||
:<math>F_n = F_{n-1}+F_{n-2}</math> |
|||
Other examples include the [[power of two]] sequence <math>1, 2, 4, 8, 16, \ldots</math>, where each number is the sum of twice the previous number, and the [[square number]] sequence <math>0, 1, 4, 9, 16, 25, \ldots</math>. All [[arithmetic progression]]s, all [[geometric progression]]s, and all [[polynomial]]s are constant-recursive. However, not all sequences are constant-recursive; for example, the [[factorial]] sequence <math>1, 1, 2, 6, 24, 120, \ldots</math> is not constant-recursive. |
|||
Constant-recursive sequences are studied in [[combinatorics]] and the theory of [[finite difference]]s. They also arise in [[algebraic number theory]], due to the relation of the sequence to [[polynomial root]]s; in the [[analysis of algorithms]], as the running time of simple [[Recursion (computer science)|recursive function]]s; and in the theory of [[formal language]]s, where they count strings up to a given length in a [[regular language]]. Constant-recursive sequences are [[closure (mathematics)|closed]] under important mathematical operations such as [[pointwise|term-wise]] [[addition]], term-wise [[multiplication]], and [[Cauchy product]]. |
|||
with [[initial condition|initial conditions]] |
|||
:<math>F_0 = 0</math> |
|||
:<math>F_1 = 1.</math> |
|||
The [[Skolem–Mahler–Lech theorem]] states that the [[Zero of a function|zeros]] of a constant-recursive sequence have a regularly repeating (eventually periodic) form. The [[Skolem problem]], which asks for an [[algorithm]] to determine whether a linear recurrence has at least one zero, is an [[List of unsolved problems in mathematics|unsolved problem in mathematics]]. |
|||
Explicitly, the recurrence yields the equations |
|||
:<math>F_2 = F_1 + F_0 = 1</math> |
|||
:<math>F_3 = F_2 + F_1 = 2</math> |
|||
:<math>F_4 = F_3 + F_2 = 3</math> |
|||
:<math>F_5 = F_4 + F_3 = 5</math> |
|||
etc. |
|||
==Definition== |
|||
We obtain the sequence of Fibonacci numbers, which begins |
|||
:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... |
|||
A '''constant-recursive sequence''' is any sequence of [[integer]]s, [[rational number]]s, [[algebraic number]]s, [[real number]]s, or [[complex number]]s <math>s_0, s_1, s_2, s_3, \ldots</math> (written as <math>(s_n)_{n=0}^\infty</math> as a shorthand) satisfying a formula of the form |
|||
It can be solved by methods described below yielding the [[Binet formula|closed-form expression]], which involves powers of the two roots of the characteristic polynomial ''t''<sup>2</sup> = ''t'' + 1; the [[generating function]] of the sequence is the [[rational function]] |
|||
: <math>\frac{t}{1-t-t^2}.</math> |
|||
<math display=block>s_n = c_1 s_{n-1} + c_2 s_{n-2} + \dots + c_d s_{n-d},</math> |
|||
===Lucas sequences=== |
|||
The sequence 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, ... of [[Lucas number]]s satisfies the same recurrence as the Fibonacci sequence but with initial conditions |
|||
:<math>L_0 = 2</math> |
|||
:<math>L_1 = 1.</math> |
|||
for all <math>n \ge d,</math> for some fixed [[coefficient]]s <math>c_1, c_2, \dots, c_d</math> ranging over the same domain as the sequence (integers, rational numbers, algebraic numbers, real numbers, or complex numbers). |
|||
More generally, every [[Lucas sequence]] is a constant-recursive sequence. |
|||
The equation is called a [[linear recurrence with constant coefficients]] of order ''d''. |
|||
The ''order'' of the sequence is the smallest positive integer <math>d</math> such that the sequence satisfies a recurrence of order ''d'', or <math>d = 0</math> for the everywhere-zero sequence. |
|||
{{cn|date=April 2024}} |
|||
The definition above allows eventually-[[periodic sequence|periodic]] sequences such as <math>1, 0, 0, 0, \ldots</math> and <math>0, 1, 0, 0, \ldots</math>. Some authors require that <math>c_d \ne 0</math>, which excludes such sequences.{{sfn|Stanley|2011|p=464}}{{sfn|Kauers|Paule|2010|p=66}}<ref name=Border>{{Citation|last1=Halava|first1=Vesa|title=Skolem's Problem – On the Border between Decidability and Undecidability|date=2005|last2=Harju|first2=Tero|last3=Hirvensalo|first3=Mika|last4=Karhumäki|first4=Juhani|citeseerx=10.1.1.155.2606|page=1}}</ref> |
|||
===Eventually periodic sequences=== |
|||
A sequence that is eventually periodic with period length <math>\ell</math> is constant-recursive, since it satisfies the recurrence <math>s(n + \ell) = s(n)</math> for all <math>n \geq N</math> for some ''N''. |
|||
==Examples== |
|||
== Structure of homogeneous linear recurrence relations with constant coefficients== |
|||
An order ''d'' '''homogeneous linear recurrence relation with constant coefficients''' is an equation of the form |
|||
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" |
|||
:<math>a_n = c_1a_{n-1} + c_2a_{n-2}+\cdots+c_da_{n-d},</math> |
|||
|+ Selected examples of integer constant-recursive sequences<ref>{{Cite web |title=Index to OEIS: Section Rec - OeisWiki |url=https://oeis.org/wiki/Index_to_OEIS:_Section_Rec |access-date=2024-04-18 |website=oeis.org}}</ref> |
|||
! Name !! Order (<math>d</math>  ) !! First few values !! Recurrence (for <math>n \ge d</math> ) !! [[Generating function]] !! [[OEIS]] |
|||
|- |
|||
| Zero sequence || 0 || 0, 0, 0, 0, 0, 0, ... || <math>s_n = 0</math> || <math>\frac{0}{1}</math> || {{OEIS link|A000004}} |
|||
|- |
|||
| One sequence || 1 || 1, 1, 1, 1, 1, 1, ... || <math>s_n = s_{n-1}</math> || <math>\frac{1}{1-x}</math> || {{OEIS link|A000012}} |
|||
|- |
|||
| [[Indicator function|Characteristic function]] of <math>\{0\}</math> || 1 || 1, 0, 0, 0, 0, 0, ... || <math>s_n = 0</math> || <math>\frac{1}{1}</math> || {{OEIS link|A000007}} |
|||
|- |
|||
| [[Powers of two]] || 1 || 1, 2, 4, 8, 16, 32, ... || <math>s_n = 2 s_{n-1}</math> || <math>\frac{1}{1-2x}</math> || {{OEIS link|A000079}} |
|||
|- |
|||
| Powers of −1|| 1 || 1, −1, 1, −1, 1, −1, ... || <math>s_n = -s_{n-1}</math> || <math>\frac{1}{1+x}</math> || {{OEIS link|A033999}} |
|||
|- |
|||
| Characteristic function of <math>\{1\}</math> || 2 || 0, 1, 0, 0, 0, 0, ... || <math>s_n = 0</math> || <math>\frac{x}{1}</math> || {{OEIS link|A063524}} |
|||
|- |
|||
| [[Decimal representation|Decimal expansion]] of 1/6 || 2 || 1, 6, 6, 6, 6, 6, ... || <math>s_n = s_{n-1}</math> || <math>\frac{1 + 5x}{1 - x}</math> || {{OEIS link|A020793}} |
|||
|- |
|||
| Decimal expansion of 1/11 || 2 || 0, 9, 0, 9, 0, 9, ... || <math>s_n = s_{n-2}</math> || <math>\frac{9x}{1-x^2}</math> || {{OEIS link|A010680}} |
|||
|- |
|||
| [[Natural number|Nonnegative integers]] || 2 || 0, 1, 2, 3, 4, 5, ... || <math>s_n = 2s_{n-1} - s_{n-2}</math> || <math>\frac{x}{(1-x)^2}</math> || {{OEIS link|A001477}} |
|||
|- |
|||
| [[Parity (mathematics)|Odd]] positive integers || 2 || 1, 3, 5, 7, 9, 11, ... || <math>s_n = 2s_{n-1} - s_{n-2}</math> || <math>\frac{1+x}{(1-x)^2}</math> || {{OEIS link|A005408}} |
|||
|- |
|||
| [[Fibonacci number]]s || 2 || 0, 1, 1, 2, 3, 5, 8, 13, ... || <math>s_n = s_{n-1} + s_{n-2}</math> || <math>\frac{x}{1-x-x^2}</math> || {{OEIS link|A000045}} |
|||
|- |
|||
| [[Lucas number]]s || 2 || 2, 1, 3, 4, 7, 11, 18, 29, ... || <math>s_n = s_{n-1} + s_{n-2}</math> || <math>\frac{2-x}{1-x-x^2}</math> || {{OEIS link|A000032}} |
|||
|- |
|||
| [[Pell number]]s || 2 || 0, 1, 2, 5, 12, 29, 70, ... || <math>s_n = 2s_{n-1} + s_{n-2}</math> || <math>\frac{x}{1-2x-x^2}</math> || {{OEIS link|A000129}} |
|||
|- |
|||
| Powers of two [[Interleave sequence|interleaved with]] 0s || 2 || 1, 0, 2, 0, 4, 0, 8, 0, ... || <math>s_n = 2 s_{n-2}</math> || <math>\frac{1}{1-2x^2}</math> || {{OEIS link|A077957}} |
|||
|- |
|||
| Inverse of 6th [[cyclotomic polynomial]] || 2 || 1, 1, 0, −1, −1, 0, 1, 1, ... || <math>s_n = s_{n-1} - s_{n-2}</math> || <math>\frac{1}{1-x+x^2}</math> || {{OEIS link|A010892}} |
|||
|- |
|||
| [[Triangular number]]s || 3 || 0, 1, 3, 6, 10, 15, 21, ... || <math>s_n = 3s_{n-1} - 3s_{n-2} + s_{n-3}</math> || <math>\frac{x}{(1-x)^3}</math> || {{OEIS link|A000217}} |
|||
|} |
|||
===Fibonacci and Lucas sequences=== |
|||
where the ''d'' coefficients ''c<sub>i</sub>'' (for all ''i'') are constants. |
|||
The sequence 0, 1, 1, 2, 3, 5, 8, 13, ... of [[Fibonacci number]]s is constant-recursive of order 2 because it satisfies the recurrence <math>F_n = F_{n-1} + F_{n-2}</math> with <math>F_0 = 0, F_1 = 1</math>. For example, <math>F_2 = F_1 + F_0 = 1 + 0 = 1</math> and <math>F_6 = F_5 + F_4 = 5 + 3 = 8</math>. The sequence 2, 1, 3, 4, 7, 11, ... of [[Lucas number]]s satisfies the same recurrence as the Fibonacci sequence but with initial conditions <math>L_0 = 2</math> and <math>L_1 = 1</math>. More generally, every [[Lucas sequence]] is constant-recursive of order 2.{{sfn|Kauers|Paule|2010|p=70}} |
|||
===Arithmetic progressions=== |
|||
More precisely, this is an infinite list of simultaneous linear equations, one for each ''n''>''d''−1. A sequence that satisfies a relation of this form is called a '''linear recurrence sequence''' or LRS. There are ''d'' [[Degrees of freedom (statistics)|degrees of freedom]] for LRS, i.e., the initial values <math>a_0,\dots,a_{d-1}</math> can be taken to be any values but then the linear recurrence determines the sequence uniquely. |
|||
For any <math>a</math> and any <math>r \ne 0</math>, the [[arithmetic progression]] <math>a, a+r, a+2r, \ldots</math> is constant-recursive of order 2, because it satisfies <math>s_n = 2s_{n-1} - s_{n-2}</math>. Generalizing this, see [[Constant-recursive sequence#Polynomial sequences|polynomial sequences]] below. |
|||
{{cn|date=April 2024}} |
|||
===Geometric progressions=== |
|||
The same coefficients yield the [[characteristic polynomial]] (also "auxiliary polynomial") |
|||
For any <math>a \ne 0</math> and <math>r</math>, the [[geometric progression]] <math>a, a r, a r^2, \ldots</math> is constant-recursive of order 1, because it satisfies <math>s_n = r s_{n-1}</math>. This includes, for example, the sequence 1, 2, 4, 8, 16, ... as well as the rational number sequence <math display=inline>1, \frac12, \frac14, \frac18, \frac{1}{16}, ...</math>. |
|||
{{cn|date=April 2024}} |
|||
===Eventually periodic sequences=== |
|||
:<math>p(t)= t^d - c_1t^{d-1} - c_2t^{d-2}-\cdots-c_{d}</math> |
|||
A sequence that is eventually periodic with period length <math>\ell</math> is constant-recursive, since it satisfies <math>s_n = s_{n-\ell}</math> for all <math>n \geq d</math>, where the order <math>d</math> is the length of the initial segment including the first repeating block. Examples of such sequences are 1, 0, 0, 0, ... (order 1) and 1, 6, 6, 6, ... (order 2). |
|||
whose ''d'' roots play a crucial role in finding and understanding the sequences satisfying the recurrence. If the roots ''r''<sub>1</sub>, ''r''<sub>2</sub>, ... are all distinct, then the solution to the recurrence takes the form |
|||
{{cn|date=April 2024}} |
|||
:<math>a_n = k_1 r_1^n + k_2 r_2^n + \cdots + k_d r_d^n,</math> |
|||
where the coefficients ''k<sub>i</sub>'' are determined in order to fit the initial conditions of the recurrence. When the same roots occur multiple times, the terms in this formula corresponding to the second and later occurrences of the same root are multiplied by increasing powers of ''n''. For instance, if the characteristic polynomial can be factored as (''x''−''r'')<sup>3</sup>, with the same root ''r'' occurring three times, then the solution would take the form |
|||
:<math>a_n = k_1 r^n + k_2 n r^n + k_3 n^2 r^n.</math><ref>{{citation|contribution=2.1.1 Constant coefficients – A) Homogeneous equations|title=Mathematics for the Analysis of Algorithms|first1=Daniel H.|last1=Greene|first2=Donald E.|last2=Knuth|author2-link=Donald Knuth| edition=2nd| publisher=Birkhäuser |page=17 | year=1982}}.</ref> |
|||
===Polynomial sequences=== |
|||
=== Rational generating function === |
|||
A sequence defined by a polynomial <math>s_n = a_0 + a_1 n + a_2 n^2 + \cdots + a_d n^d</math> is constant-recursive. The sequence satisfies a recurrence of order <math>d + 1</math> (where <math>d</math> is the [[degree of a polynomial|degree]] of the polynomial), with coefficients given by the corresponding element of the [[binomial transform]].<ref>{{Cite journal|last=Boyadzhiev|first=Boyad|date=2012|title=Close Encounters with the Stirling Numbers of the Second Kind|url=https://www.maa.org/sites/default/files/pdf/upload_library/2/Boyadzhiev-2013.pdf|journal=Math. Mag.|volume=85|issue=4|pages=252–266|doi=10.4169/math.mag.85.4.252|arxiv=1806.09468|s2cid=115176876}}</ref><ref>{{Cite journal |last=Riordan |first=John |date=1964 |title=Inverse Relations and Combinatorial Identities |url=https://www.tandfonline.com/doi/full/10.1080/00029890.1964.11992269 |journal=The American Mathematical Monthly |language=en |volume=71 |issue=5 |pages=485–498 |doi=10.1080/00029890.1964.11992269 |issn=0002-9890}}</ref> The first few such equations are |
|||
Theorem: Linear recursive sequences are precisely the sequences whose [[generating function]] is a [[rational function]]. The denominator is the polynomial obtained from the auxiliary polynomial by reversing the order of the coefficients, and the numerator is determined by the initial values of the sequence.<ref>{{Cite journal|title = On the variety of linear recurrences and numerical semigroups|url = http://link.springer.com/article/10.1007/s00233-013-9551-2|journal = [[Semigroup Forum]]|date = 2013-11-14|issn = 0037-1912|pages = 569-574|volume = 88|issue = 3|doi = 10.1007/s00233-013-9551-2|language = en|first = Ivan|last = Martino|first2 = Luca|last2 = Martino}}</ref> |
|||
: <math>s_n = 1 \cdot s_{n-1}</math> for a degree 0 (that is, constant) polynomial, |
|||
The simplest cases are periodic sequences, <math>a_n = a_{n-d}, n\geq d</math>, which have sequence <math>a_0,a_1,\dots,a_{d-1},a_0,\dots</math> and generating function a sum of geometric series: |
|||
: <math>s_n = 2\cdot s_{n-1} - 1\cdot s_{n-2}</math> for a degree 1 or less polynomial, |
|||
:<math>\begin{align}\frac{a_0 + a_1 x^1 + \cdots + a_{d-1}x^{d-1}}{1-x^d} =& \left(a_0 + a_1 x^1 + \cdots + a_{d-1}x^{d-1}\right) + \left(a_0 + a_1 x^1 + \cdots + a_{d-1}x^{d-1}\right)x^d + \\& \left(a_0 + a_1 x^1 + \cdots + a_{d-1}x^{d-1}\right)x^{2d} + \cdots.\end{align}</math> |
|||
: <math>s_n = 3\cdot s_{n-1} - 3\cdot s_{n-2} + 1\cdot s_{n-3}</math> for a degree 2 or less polynomial, and |
|||
: <math>s_n = 4\cdot s_{n-1} - 6\cdot s_{n-2} + 4\cdot s_{n-3} - 1\cdot s_{n-4}</math> for a degree 3 or less polynomial. |
|||
A sequence obeying the order-''d'' equation also obeys all higher order equations. These identities may be [[mathematical proof|proved]] in a number of ways, including via the theory of [[finite difference]]s.<ref>{{Cite book|last1=Jordan|first1=Charles|url=https://books.google.com/books?id=3RfZOsDAyQsC&dq=theory+of+finite+differences&pg=PA1|title=Calculus of Finite Differences|last2=Jordán|first2=Károly|date=1965|publisher=American Mathematical Soc.|isbn=978-0-8284-0033-6|language=en|pages=9–11}} See formula on p.9, top.</ref> |
|||
More generally, given the recurrence relation: |
|||
Any sequence of <math>d + 1</math> integer, real, or complex values can be used as initial conditions for a constant-recursive sequence of order <math>d + 1</math>. If the initial conditions lie on a polynomial of degree <math>d - 1</math> or less, then the constant-recursive sequence also obeys a lower order equation. |
|||
:<math>a_n = c_1a_{n-1} + c_2a_{n-2}+\cdots+c_da_{n-d}</math> |
|||
with generating function |
|||
===Enumeration of words in a regular language=== |
|||
:<math>a_0 + a_1x^1 + a_2 x^2 + \cdots,</math> |
|||
Let <math>L</math> be a [[regular language]], and let <math>s_n</math> be the number of words of length <math>n</math> in <math>L</math>. Then <math>(s_n)_{n=0}^\infty</math> is constant-recursive.{{sfn|Kauers|Paule|2010|p=81}} For example, <math>s_n = 2^n</math> for the language of all binary strings, <math>s_n = 1</math> for the language of all unary strings, and <math>s_n = F_{n+2}</math> for the language of all binary strings that do not have two consecutive ones. More generally, any function accepted by a [[weighted automaton]] over the unary alphabet <math>\Sigma = \{a\}</math> over the [[semiring]] <math>(\mathbb{R}, +, \times)</math> (which is in fact a [[ring (mathematics)|ring]], and even a [[field (mathematics)|field]]) is constant-recursive. |
|||
the series is annihilated at ''a<sub>d</sub>'' and above by the polynomial: |
|||
{{cn|date=April 2024}} |
|||
===Other examples=== |
|||
:<math>1- c_1x^1 - c_2 x^2 - \cdots - c_dx^d.</math> |
|||
The sequences of [[Jacobsthal number]]s, [[Padovan number]]s, [[Pell number]]s, and [[Perrin number]]s{{sfn|Kauers|Paule|2010|p=70}} are constant-recursive. |
|||
That is, multiplying the generating function by the polynomial yields |
|||
===Non-examples=== |
|||
:<math>b_n = a_n - c_1 a_{n-1} - c_2 a_{n-2} - \cdots - c_d a_{n-d}</math> |
|||
The [[factorial]] sequence <math>1, 1, 2, 6, 24, 120, 720, \ldots</math> is not constant-recursive. More generally, every constant-recursive function is asymptotically bounded by an [[exponential function]] (see [[#Closed-form characterization]]) and the factorial sequence grows faster than this. |
|||
as the coefficient on <math>x^n</math>, which vanishes (by the recurrence relation) for ''n'' ≥ ''d''. Thus |
|||
The [[Catalan sequence]] <math>1, 1, 2, 5, 14, 42, 132, \ldots</math> is not constant-recursive. This is because the [[Catalan number#First proof|generating function of the Catalan numbers]] is not a [[rational function]] (see [[#Equivalent definitions]]). |
|||
:<math>\left (a_0 + a_1x^1 + a_2 x^2 + \cdots \right ) \left (1- c_1x^1 - c_2 x^2 - \cdots - c_dx^d \right) = \left (b_0 + b_1x^1 + b_2 x^2 + \cdots + b_{d-1} x^{d-1} \right )</math> |
|||
==Equivalent definitions== |
|||
so dividing yields |
|||
===In terms of matrices=== |
|||
:<math>a_0 + a_1x^1 + a_2 x^2 + \cdots =\frac{b_0 + b_1x^1 + b_2 x^2 + \cdots + b_{d-1} x^{d-1}}{1- c_1x^1 - c_2 x^2 - \cdots - c_dx^d},</math> |
|||
{{main|Companion matrix}} |
|||
expressing the generating function as a rational function. |
|||
{{float begin|width=195px|side=right}} |
|||
|-style="text-align:center;" |
|||
| <math>F_n = \begin{bmatrix}0 & 1\end{bmatrix} |
|||
\begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix}^n |
|||
\begin{bmatrix}1 \\ 0\end{bmatrix}.</math> |
|||
{{float end|Definition of the Fibonacci sequence using matrices.}} |
|||
A sequence <math>(s_n)_{n=0}^\infty</math> is constant-recursive of order less than or equal to <math>d</math> if and only if it can be written as |
|||
The denominator is <math>x^d p\left(x^{-1}\right),</math> a transform of the auxiliary polynomial (equivalently, reversing the order of coefficients); one could also use any multiple of this, but this normalization is chosen both because of the simple relation to the auxiliary polynomial, and so that <math>b_0 = a_0</math>. |
|||
:<math>s_n = u A^n v</math> |
|||
where <math>u</math> is a <math>1 \times d</math> vector, <math>A</math> is a <math>d \times d</math> [[matrix (mathematics)|matrix]], and <math>v</math> is a <math>d \times 1</math> vector, where the elements come from the same domain (integers, rational numbers, algebraic numbers, real numbers, or complex numbers) as the original sequence. Specifically, <math>v</math> can be taken to be the first <math>d</math> values of the sequence, <math>A</math> the [[linear transformation]] that computes <math>s_{n+1}, s_{n+2}, \ldots, s_{n+d}</math> from <math>s_n, s_{n+1}, \ldots, s_{n+d-1}</math>, and <math>u</math> the vector <math>[0, 0, \ldots, 0, 1]</math>.<ref name="ow"/> |
|||
===In terms of non-homogeneous linear recurrences=== |
|||
The [[Catalan number#First proof|generating function of the Catalan numbers]] is not a rational function, so the theorem tells us that the [[Catalan numbers]] do not satisfy a linear recurrence with constant coefficients. |
|||
{{main|Linear recurrence with constant coefficients#Conversion to homogeneous form}} |
|||
{{float begin|width=250px|side=right}} |
|||
|- class="wikitable" |
|||
! Non-homogeneous !! Homogeneous |
|||
|- align = "center" |
|||
| <math>s_n = 1 + s_{n-1}</math> |
|||
| <math>s_n = 2s_{n-1} - s_{n-2}</math> |
|||
|- align = "center" |
|||
| <math>s_0 = 0</math> |
|||
| <math>s_0 = 0; s_1 = 1</math> |
|||
{{float end|Definition of the sequence of [[natural number]]s <math>s_n = n</math>, using a non-homogeneous recurrence and the equivalent homogeneous version.}} |
|||
A '''non-homogeneous linear recurrence''' is an equation of the form |
|||
For order 1, the recurrence |
|||
:<math> |
:<math>s_n = c_1 s_{n-1} + c_2 s_{n-2} + \dots + c_d s_{n-d} + c</math> |
||
where <math>c</math> is an additional constant. Any sequence satisfying a non-homogeneous linear recurrence is constant-recursive. This is because subtracting the equation for <math>s_{n-1}</math> from the equation for <math>s_n</math> yields a homogeneous recurrence for <math>s_n - s_{n-1}</math>, from which we can solve for <math>s_n</math> to obtain{{cn|date=April 2024}} |
|||
has the solution ''a<sub>n</sub>'' = ''r<sup>n</sup>'' with ''a''<sub>0</sub> = 1 and the most general solution is ''a<sub>n</sub>'' = ''kr<sup>n</sup>'' with ''a''<sub>0</sub> = ''k''. The characteristic polynomial equated to zero (the [[Characteristic polynomial|characteristic equation]]) is simply ''t'' − ''r'' = 0. |
|||
:<math>\begin{align}s_n = &(c_1 + 1) s_{n-1} \\ &+ (c_2 - c_1) s_{n-2} + \dots + (c_d - c_{d-1}) s_{n-d} \\&- c_d s_{n-d-1}.\end{align}</math> |
|||
=== In terms of generating functions === |
|||
Solutions to such recurrence relations of higher order are found by systematic means, often using the fact that ''a<sub>n</sub>'' = ''r<sup>n</sup>'' is a solution for the recurrence exactly when ''t'' = ''r'' is a root of the characteristic polynomial. This can be approached directly or using [[generating function]]s ([[formal power series]]) or matrices. |
|||
{{float begin|width=180px|side=right}} |
|||
Consider, for example, a recurrence relation of the form |
|||
|-style="text-align:center;" |
|||
|<math>\sum_{n = 0}^\infty F_n x^n = \frac{x}{1-x-x^2}.</math> |
|||
{{float end|caption=Definition of the Fibonacci sequence using a generating function.}} |
|||
A sequence is constant-recursive precisely when its [[generating function]] |
|||
:<math>a_{n}=Aa_{n-1}+Ba_{n-2}.</math> |
|||
:<math>\sum_{n = 0}^\infty s_n x^n = s_0 + s_1 x^1 + s_2 x^2 + s_3 x^3 + \cdots</math> |
|||
is a rational function <math>p(x) \,/\, q(x)</math>, where <math>p</math> and <math>q</math> are polynomials and <math>q(0) = 1</math>.{{sfn|Stanley|2011|p=464}} |
|||
When does it have a solution of the same general form as ''a<sub>n</sub>'' = ''r<sup>n</sup>''? Substituting this guess ([[ansatz]]) in the recurrence relation, we find that |
|||
Moreover, the order of the sequence is the minimum <math>d</math> such that it has such a form with <math>\text{deg } q(x) \le d</math> and <math>\text{deg } p(x) < d</math>.{{sfn|Stanley|2011|pp=464-465}} |
|||
:<math>r^{n}=Ar^{n-1}+Br^{n-2}</math> |
|||
must be true for '''all''' ''n'' > 1. |
|||
Dividing through by ''r''<sup>''n''−2</sup>, we get that all these equations reduce to the same thing: |
|||
:<math>r^2=Ar+B,</math> |
|||
:<math>r^2-Ar-B=0,</math> |
|||
which is the characteristic equation of the recurrence relation. Solve for ''r'' to obtain the two roots ''λ''<sub>1</sub>, ''λ''<sub>2</sub>: these roots are known as the [[characteristic root]]s or '''eigenvalues''' of the characteristic equation. Different solutions are obtained depending on the nature of the roots: If these roots are distinct, we have the general solution |
|||
:<math>a_n = C\lambda_1^n+D\lambda_2^n</math> |
|||
while if they are identical (when ''A''<sup>2</sup> + 4''B'' = 0), we have |
|||
:<math>a_n = C\lambda^n+Dn\lambda^n</math> |
|||
This is the most general solution; the two constants ''C'' and ''D'' can be chosen based on two given initial conditions ''a''<sub>0</sub> and ''a''<sub>1</sub> to produce a specific solution. |
|||
In the case of complex eigenvalues (which also gives rise to complex values for the solution parameters ''C'' and ''D''), the use of complex numbers can be eliminated by rewriting the solution in trigonometric form. In this case we can write the eigenvalues as <math>\lambda_1, \lambda_2 = \alpha \pm \beta i.</math> Then it can be shown that |
|||
:<math>a_n = C\lambda_1^n+D\lambda_2^n</math> |
|||
can be rewritten as<ref>Chiang, Alpha C., ''Fundamental Methods of Mathematical Economics'', third edition, McGraw-Hill, 1984.</ref>{{rp|576–585}} |
|||
:<math>a_n = 2 M^n \left( E \cos(\theta n) + F \sin(\theta n)\right) = 2 G M^n \cos(\theta n - \delta),</math> |
|||
The denominator is the polynomial obtained from the auxiliary polynomial by [[reciprocal polynomial|reversing the order of the coefficients]], and the numerator is determined by the initial values of the sequence:<ref>{{Cite journal|title = On the variety of linear recurrences and numerical semigroups|journal = [[Semigroup Forum]]|date = 2013-11-14|issn = 0037-1912|pages = 569–574|volume = 88|issue = 3|doi = 10.1007/s00233-013-9551-2|language = en|first1 = Ivan|last1 = Martino|first2 = Luca|last2 = Martino|arxiv = 1207.0111|s2cid = 119625519}}</ref>{{sfn|Kauers|Paule|2010|p=74}} |
|||
:<math>\sum_{n = 0}^\infty s_n x^n = \frac{b_0 + b_1 x^1 + b_2 x^2 + \dots + b_{d-1} x^{d-1}}{1 - c_1 x^1 - c_2 x^2 - \dots - c_d x^d},</math> |
|||
where |
where |
||
:<math>b_n = s_n - c_1 s_{n-1} - c_2 s_{n-2} - \dots - c_d s_{n-d}.</math>{{sfn|Stanley|2011|pp=468-469}} |
|||
It follows from the above that the denominator <math>q(x)</math> must be a polynomial not divisible by <math>x</math> (and in particular nonzero). |
|||
===In terms of sequence spaces=== |
|||
:<math>\begin{array}{lcl} |
|||
M = \sqrt{\alpha^2+\beta^2} & \cos (\theta) =\tfrac{\alpha}{M} & \sin( \theta) = \tfrac{\beta}{M} \\ |
|||
C,D = E \mp F i & & \\ |
|||
G = \sqrt{E^2+F^2} & \cos (\delta ) = \tfrac{E}{G} & \sin (\delta )= \tfrac{F}{G} |
|||
\end{array}</math> |
|||
{{float begin|width=175px|side=right}} |
|||
Here ''E'' and ''F'' (or equivalently, ''G'' and δ) are real constants which depend on the initial conditions. Using |
|||
|-align=center |
|||
:<math>\lambda_1+\lambda_2=2 \alpha = A,</math> |
|||
|<math>\{(a n + b)_{n=0}^\infty : a, b \in \mathbb{R}\}</math> |
|||
{{float end|2-dimensional [[sequence space|vector space of sequences]] generated by the sequence <math>s_n = n</math>.}} |
|||
A sequence <math>(s_n)_{n=0}^\infty</math> is constant-recursive if and only if the set of sequences |
|||
one may simplify the solution given above as |
|||
:<math>\left\{(s_{n+r})_{n=0}^\infty : r \geq 0\right\}</math> |
|||
is contained in a [[sequence space]] ([[vector space]] of sequences) whose [[Dimension (vector space)|dimension]] is finite. That is, <math>(s_n)_{n=0}^\infty</math> is contained in a finite-dimensional [[Linear subspace|subspace]] of <math>\mathbb{C}^\mathbb{N}</math> [[Closure (mathematics)|closed]] under the [[Shift operator#Sequences|left-shift operator]].{{sfn|Kauers|Paule|2010|p=67}}{{sfn|Stanley|2011|p=465}} |
|||
This characterization is because the order-<math>d</math> linear recurrence relation can be understood as a [[Linear independence#Definition|proof of linear dependence]] between the sequences <math>(s_{n+r})_{n=0}^\infty</math> for <math>r=0, \ldots, d</math>. An extension of this argument shows that the order of the sequence is equal to the dimension of the sequence space generated by <math>(s_{n+r})_{n=0}^\infty</math> for all <math>r</math>.{{sfn|Kauers|Paule|2010|p=69}}{{sfn|Stanley|2011|p=465}} |
|||
:<math>a_n = (-B)^{\frac{n}{2}} \left( E \cos(\theta n) + F \sin(\theta n)\right),</math> |
|||
== Closed-form characterization == |
|||
where ''a''<sub>1</sub> and ''a''<sub>2</sub> are the initial conditions and |
|||
{{for|a derivation of the closed form|Linear recurrence with constant coefficients#General solution}} |
|||
:<math>\begin{align} |
|||
E &=\frac{-A a_1 + a_2}{B} \\ |
|||
F &=-i \frac{A^2 a_1 - A a_2 +2 a_1 B}{B \sqrt{A^2+4B}} \\ |
|||
\theta &=\arccos \left (\frac{A}{2 \sqrt{-B}} \right ) |
|||
\end{align}</math> |
|||
{{float_begin|side=right|width=300px}} |
|||
In this way there is no need to solve for λ<sub>1</sub> and λ<sub>2</sub>. |
|||
|-align=center |
|||
|<math>F_n = \frac{1}{\sqrt{5}}(1.618\ldots)^n - \frac{1}{\sqrt{5}}(-0.618\ldots)^n</math> |
|||
{{float_end|Closed-form characterization of the Fibonacci sequence ([[Fibonacci number#Binet's formula|Binet's formula]])}} |
|||
Constant-recursive sequences admit the following unique [[Closed-form expression|closed form]] characterization using [[exponential polynomial]]s: every constant-recursive sequence can be written in the form |
|||
In all cases—real distinct eigenvalues, real duplicated eigenvalues, and complex conjugate eigenvalues—the equation is [[stability theory|stable]] (that is, the variable ''a'' converges to a fixed value [specifically, zero]) if and only if ''both'' eigenvalues are smaller than one in [[absolute value]]. In this second-order case, this condition on the eigenvalues can be shown<ref>Papanicolaou, Vassilis, "On the asymptotic stability of a class of linear difference equations," ''Mathematics Magazine'' 69(1), February 1996, 34–43.</ref> to be equivalent to |''A''| < 1 − ''B'' < 2, which is equivalent to |''B''| < 1 and |''A''| < 1 − ''B''. |
|||
:<math>s_n = z_n + k_1(n) r_1^n + k_2(n) r_2^n + \cdots + k_e(n) r_e^n,</math> |
|||
for all <math>n \ge 0</math>, where |
|||
* The term <math>z_n</math> is a sequence which is zero for all <math>n \ge d</math> (where <math>d</math> is the order of the sequence); |
|||
* The terms <math>k_1(n), k_2(n), \ldots, k_e(n)</math> are complex polynomials; and |
|||
* The terms <math>r_1, r_2, \ldots, r_k</math> are distinct complex constants.{{sfn|Brousseau|1971|pp=28-34|loc=Lesson 5}}{{sfn|Stanley|2011|p=464}} |
|||
This characterization is exact: every sequence of complex numbers that can be written in the above form is constant-recursive.{{sfn|Kauers|Paule|2010|pp=68-70}} |
|||
The equation in the above example was [[homogeneous differential equation|homogeneous]], in that there was no constant term. If one starts with the non-homogeneous recurrence |
|||
For example, the Fibonacci number <math>F_n</math> is written in this form using [[Fibonacci number#Binet's formula|Binet's formula]]:{{sfn|Brousseau|1971|p=16|loc=Lesson 3}} |
|||
:<math>b_{n}=Ab_{n-1}+Bb_{n-2}+K</math> |
|||
:<math>F_n = \frac{1}{\sqrt{5}}\varphi^n - \frac{1}{\sqrt{5}}\psi^n,</math> |
|||
where <math>\varphi = (1 + \sqrt{5}) \,/\, 2 \approx 1.61803\ldots</math> is the [[golden ratio]] and <math>\psi = -1 \,/\, \varphi</math>. These are the roots of the equation <math>x^2 - x - 1 = 0</math>. In this case, <math>e=2</math>, <math>z_n = 0</math> for all <math>n</math>, <math>k_1(n) = k_2(n) = 1 \,/\, \sqrt{5}</math> are both constant polynomials, <math>r_1 = \varphi</math>, and <math>r_2 = \psi</math>. |
|||
The term <math>z_n</math> is only needed when <math>c_d\ne 0</math>; if <math>c_d = 0</math> then it corrects for the fact that some initial values may be exceptions to the general recurrence. In particular, <math>z_n = 0</math> for all <math>n \ge d</math>.{{cn|date=April 2024}} |
|||
with constant term ''K'', this can be converted into homogeneous form as follows: The [[steady state]] is found by setting ''b<sub>n</sub>'' = ''b''<sub>''n''−1</sub> = ''b''<sub>''n''−2</sub> = ''b''* to obtain |
|||
The complex numbers <math>r_1, \ldots, r_n</math> are the roots of the [[characteristic equation (calculus)|characteristic polynomial]] of the recurrence: |
|||
:<math> b^{*} = \frac{K}{1-A-B}.</math> |
|||
:<math>x^d - c_1 x^{d-1} - \dots - c_{d-1} x - c_d</math> |
|||
whose coefficients are the same as those of the recurrence.{{sfn|Brousseau|1971|p=28|loc=Lesson 5}} |
|||
If the sequence consists of integers or rational numbers, the roots will be [[algebraic number]]s. |
|||
If the <math>d</math> roots <math>r_1, r_2, \dots, r_d</math> are all distinct, then the polynomials <math>k_i(n)</math> are all constants, which can be determined from the initial values of the sequence. |
|||
If the roots of the characteristic polynomial are not distinct, and <math>r_i</math> is a root of [[Multiplicity (mathematics)|multiplicity]] <math>m</math>, then <math>k_i(n)</math> in the formula has degree <math>m - 1</math>. For instance, if the characteristic polynomial factors as <math>(x-r)^3</math>, with the same root ''r'' occurring three times, then the <math>n</math>th term is of the form <math>s_n = (a + b n + c n^2) r^n.</math><ref>{{citation|contribution=2.1.1 Constant coefficients – A) Homogeneous equations|title=Mathematics for the Analysis of Algorithms|first1=Daniel H.|last1=Greene|first2=Donald E.|last2=Knuth|author2-link=Donald Knuth| edition=2nd| publisher=Birkhäuser |page=17 | year=1982}}.</ref>{{sfn|Brousseau|1971|pp=29-31|loc=Lesson 5}} |
|||
==Closure properties== |
|||
Then the non-homogeneous recurrence can be rewritten in homogeneous form as |
|||
===Examples=== |
|||
:<math>[b_n - b^*]=A[b_{n-1}-b^*]+B[b_{n-2}-b^*],</math> |
|||
The sum of two constant-recursive sequences is also constant-recursive.{{sfn|Kauers|Paule|2010|p=71}}{{sfn|Brousseau|1971|p=37|loc=Lesson 6}} For example, the sum of <math>s_n = 2^n</math> and <math>t_n = n</math> is <math>u_n = 2^n + n</math> (<math>1, 3, 6, 11, 20, \ldots</math>), which satisfies the recurrence <math>u_n = 4u_{n-1} - 5u_{n-2} + 2u_{n-3}</math>. The new recurrence can be found by adding the generating functions for each sequence. |
|||
which can be solved as above. |
|||
Similarly, the product of two constant-recursive sequences is constant-recursive.{{sfn|Kauers|Paule|2010|p=71}} For example, the product of <math>s_n = 2^n</math> and <math>t_n = n</math> is <math>u_n = n \cdot 2^n</math> (<math>0, 2, 8, 24, 64, \ldots</math>), which satisfies the recurrence <math>u_n = 4 u_{n-1} - 4 u_{n-2}</math>. |
|||
The stability condition stated above in terms of eigenvalues for the second-order case remains valid for the general ''n''<sup>th</sup>-order case: the equation is stable if and only if all eigenvalues of the characteristic equation are less than one in absolute value. |
|||
The left-shift sequence <math>u_n = s_{n + 1}</math> and the right-shift sequence <math>u_n = s_{n - 1}</math> (with <math>u_0 = 0</math>) are constant-recursive because they satisfy the same recurrence relation. For example, because <math>s_n = 2^n</math> is constant-recursive, so is <math>u_n = 2^{n + 1}</math>. |
|||
===Solving via linear algebra=== |
|||
A linearly recursive sequence y of order n |
|||
===List of operations=== |
|||
:<math>y_{n+k} - c_{n-1}y_{n-1+k} - c_{n-2}y_{n-2+k} + \cdots - c_{0}y_{k} = 0</math> |
|||
In general, constant-recursive sequences are [[Closure (mathematics)|closed]] under the following operations, where <math>s = (s_n)_{n \in \mathbb{N}}, t = (t_n)_{n \in \mathbb{N}}</math> denote constant-recursive sequences, <math>f(x), g(x)</math> are their generating functions, and <math>d, e</math> are their orders, respectively.{{sfn|Stanley|2011|pp=471}} |
|||
is identical to |
|||
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" |
|||
:<math>y_{n} = c_{n-1}y_{n-1} + c_{n-2}y_{n-2} + \cdots +c_{0}y_{0}.</math> |
|||
|+ Operations on constant-recursive sequences |
|||
! Operation !! Definition !! Requirement !! Generating function equivalent || Order |
|||
|- |
|||
| Term-wise sum <math>s + t</math> || <math>(s + t)_n = s_n + t_n</math> || — || <math>f(x) + g(x)</math> || <math>\le d + e</math>{{sfn|Kauers|Paule|2010|p=71}} |
|||
|- |
|||
| Term-wise product <math>s \cdot t</math> || <math>(s \cdot t)_n = s_n \cdot t_n</math> || — || <math>\frac{1}{2 \pi i} \int_\gamma \frac{f(\zeta)}{\zeta} g\left(\frac{x}{\zeta}\right) \; \mathrm{d}\zeta</math><ref>{{Cite journal |last=Pohlen |first=Timo |date=2009 |title=The Hadamard product and universal power series |url=https://ubt.opus.hbz-nrw.de/opus45-ubtr/frontdoor/deliver/index/docId/327/file/Dissertation.pdf |pp=36-37 |journal=University of Trier (Doctoral Dissertation)}}</ref><ref>See [[Hadamard product (series)]] and [[Parseval's theorem]].</ref> || <math> \le d \cdot e </math><ref name="ow"/>{{sfn|Kauers|Paule|2010|p=71}} |
|||
|- |
|||
| [[Cauchy product]] <math>s * t</math> || <math>(s * t)_n = \sum_{i=0}^n s_i t_{n-i}</math> || — || <math>f(x) g(x)</math> || <math>\le d + e</math>{{sfn|Stanley|2011|pp=471}} |
|||
|- |
|||
| Left shift <math>Ls</math> || <math>(Ls)_n = s_{n+1}</math> || — || <math>\frac{f(x) - s_0}{x}</math> || <math>\le d</math>{{sfn|Stanley|2011|pp=471}} |
|||
|- |
|||
| Right shift <math>Rs</math> || <math>(Rs)_n = \begin{cases}s_{n-1} &n \ge 1\\0 &n = 0\end{cases}</math> || — || <math>x f(x)</math> || <math>\le d + 1</math>{{sfn|Stanley|2011|pp=471}} |
|||
|- |
|||
| [[Formal power series#Multiplicative inverse|Cauchy inverse]] <math>s^{(-1)}</math> || <math>(s^{(-1)})_n = \sum_{{i_1 + \dots + i_k = n} \atop {i_1, \ldots, i_k \ne 0}} (-1)^k s_{i_1} s_{i_2} \cdots s_{i_k}</math> || <math>s_0 = 1</math> || <math>\frac{1}{f(x)}</math> || <math>\le d + 1</math>{{sfn|Stanley|2011|pp=471}} |
|||
|- |
|||
| [[Kleene star]] <math>s^{(*)}</math> || <math>(s^{(*)})_n = \sum_{{i_1 + \dots + i_k = n} \atop {i_1, \ldots, i_k \ne 0}} s_{i_1} s_{i_2} \cdots s_{i_k}</math> || <math> s_0 = 0</math> || <math>\frac{1}{1 - f(x)}</math> || <math>\le d + 1</math>{{sfn|Stanley|2011|pp=471}} |
|||
|} |
|||
The closure under term-wise addition and multiplication follows from the closed-form characterization in terms of exponential polynomials. The closure under Cauchy product follows from the generating function characterization.{{sfn|Stanley|2011|pp=471}} The requirement <math>s_0 = 1</math> for Cauchy inverse is necessary for the case of integer sequences, but can be replaced by <math>s_0 \ne 0</math> if the sequence is over any [[field (mathematics)|field]] (rational, algebraic, real, or complex numbers).{{sfn|Stanley|2011|pp=471}} |
|||
Expanded with n-1 identities of kind <math>y_{n-k} = y_{n-k},</math> this n-th order equation is translated into a system of n first order linear equations, |
|||
<!-- |
|||
TBD: closure operations characterization: |
|||
:<math>\vec y_{n} = \begin{bmatrix}y_n\\y_{n-1}\\ \vdots \\ \vdots \\ y_1 \end{bmatrix} = |
|||
The constant-recursive sequences can be characterized as the smallest set of sequences containing the constants (in integer, rational, algebraic, or complex numbers) closed under pointwise addition, right-shift, Cauchy product, and either Cauchy inverse or Kleene star. |
|||
A characterization involving product might also be possible. |
|||
Need to include a citation for these statements. |
|||
--> |
|||
==Behavior== |
|||
\begin{bmatrix} |
|||
c_{n-1} & c_{n-2} & \cdots & \cdots & c_{0} \\ |
|||
1 & 0 & \cdots & \cdots & 0 \\ |
|||
0 & \ddots & \ddots & &\vdots \\ |
|||
\vdots & \ddots & \ddots & \ddots &\vdots \\ |
|||
0 & \cdots & 0 & 1 & 0 \end{bmatrix} |
|||
{{main|Skolem–Mahler–Lech theorem|Skolem problem}} |
|||
\begin{bmatrix}y_{n-1} \\y_{n-2} \\ \vdots \\ \vdots \\ y_0 \end{bmatrix} |
|||
{{Unsolved|mathematics|Is there an algorithm to test whether a constant-recursive sequence has a zero?}} |
|||
= C\ \vec y_{n-1} = C^n \vec y_0.</math> |
|||
===Zeros=== |
|||
Observe that the vector <math>\vec y_n</math> can be computed by ''n'' applications of the [[companion matrix]], C, to the initial state vector, <math>y_0</math>. Thereby, n-th entry of the sought sequence y, is the top component of <math>\vec y_n, y_n = \vec y_n[n]</math>. |
|||
Despite satisfying a simple local formula, a constant-recursive sequence can exhibit complicated global behavior. Define a ''zero'' of a constant-recursive sequence to be a nonnegative integer <math>n</math> such that <math>s_n = 0</math>. The Skolem–Mahler–Lech theorem states that the zeros of the sequence are eventually repeating: there exists constants <math>M</math> and <math>N</math> such that for all <math>n > M</math>, <math>s_n = 0</math> if and only if <math>s_{n+N} = 0</math>. This result holds for a constant-recursive sequence over the complex numbers, or more generally, over any [[Field (mathematics)|field]] of [[Characteristic (algebra)|characteristic]] zero.<ref>{{citation|last=Lech|first=C.|title=A Note on Recurring Series|journal=Arkiv för Matematik|volume=2|pages=417–421|year=1953|issue=5|doi=10.1007/bf02590997|bibcode=1953ArM.....2..417L |doi-access=free}}</ref> |
|||
===Decision problems=== |
|||
[[Eigendecomposition of a matrix#Example|Eigendecomposition]], <math>\vec y_n = \vec C^n\, \vec y_0 = c_1\,\lambda_1^n\,\vec e_1 + c_2\,\lambda_2^n\,\vec e_2 + \cdots + c_n\,\lambda_n^n\,\vec e_n</math> into eigenvalues, <math>\lambda_1, \lambda_2, \ldots, \lambda_n</math>, and eigenvectors, <math>\vec e_1, \vec e_2, \ldots, \vec e_n</math>, is used to compute <math>\vec y_n.</math> Thanks to the crucial fact that system ''C'' time-shifts every eigenvector, ''e'', by simply scaling its components ''λ'' times, |
|||
The pattern of zeros in a constant-recursive sequence can also be investigated from the perspective of [[computability theory]]. To do so, the description of the sequence <math>s_n</math> must be given a [[String (computer science)|finite description]]; this can be done if the sequence is over the integers or rational numbers, or even over the algebraic numbers.<ref name="ow">{{citation |
|||
| last1 = Ouaknine | first1 = Joël |
|||
| last2 = Worrell | first2 = James |
|||
| contribution = Decision problems for linear recurrence sequences |
|||
| doi = 10.1007/978-3-642-33512-9_3 |
|||
| mr = 3040104 |
|||
| pages = 21–28 |
|||
| publisher = Springer-Verlag | location = Heidelberg |
|||
| series = Lecture Notes in Computer Science |
|||
| title = Reachability Problems: 6th International Workshop, RP 2012, Bordeaux, France, September 17–19, 2012, Proceedings |
|||
| volume = 7550 |
|||
| year = 2012| isbn = 978-3-642-33511-2 |
|||
}}.</ref> |
|||
Given such an encoding for sequences <math>s_n</math>, the following problems can be studied: |
|||
{| class="wikitable" style="margin-left: auto; margin-right: auto; border: none;" |
|||
:<math>C\,\vec e_i = \lambda_i \vec e_i = C \begin{bmatrix}e_{i,n} \\e_{i,n-1} \\ \vdots \\ e_{i,1}\end{bmatrix} = \begin{bmatrix}\lambda_i\,e_{i,n} \\ \lambda_i\,e_{i,n-1} \\ \vdots \\ \lambda_i\,e_{i,1}\end{bmatrix}</math> |
|||
|+ Notable decision problems |
|||
! Problem !! Description !! Status<ref name="ow"/><ref name=LICS22>{{Cite book |last1=Lipton |first1=Richard |last2=Luca |first2=Florian |last3=Nieuwveld |first3=Joris |last4=Ouaknine |first4=Joël |last5=Purser |first5=David |last6=Worrell |first6=James |chapter=On the Skolem Problem and the Skolem Conjecture |date=2022-08-04 |title=Proceedings of the 37th Annual ACM/IEEE Symposium on Logic in Computer Science |chapter-url=https://dl.acm.org/doi/10.1145/3531130.3533328 |series=LICS '22 |location=New York, NY, USA |publisher=Association for Computing Machinery |pages=1–9 |doi=10.1145/3531130.3533328 |isbn=978-1-4503-9351-5}}</ref> |
|||
|- |
|||
| Existence of a zero ([[Skolem problem]]) |
|||
|| On input <math>(s_n)_{n=0}^\infty</math>, is <math>s_n = 0</math> for some <math>n</math>? |
|||
|| Open |
|||
|- |
|||
| Infinitely many zeros |
|||
|| On input <math>(s_n)_{n=0}^\infty</math>, is <math>s_n = 0</math> for infinitely many <math>n</math>? |
|||
|| Decidable |
|||
|- |
|||
| Eventually all zero |
|||
|| On input <math>(s_n)_{n=0}^\infty</math>, is <math>s_n = 0</math> for all [[Eventually (mathematics)|sufficiently large]] <math>n</math>? |
|||
|| Decidable |
|||
|- |
|||
| Positivity |
|||
|| On input <math>(s_n)_{n=0}^\infty</math>, is <math>s_n > 0</math> for all <math>n</math>? |
|||
|| Open |
|||
|- |
|||
| Eventual positivity |
|||
|| On input <math>(s_n)_{n=0}^\infty</math>, is <math>s_n > 0</math> for all [[Eventually (mathematics)|sufficiently large]] <math>n</math>? |
|||
|| Open |
|||
|} |
|||
Because the square of a constant-recursive sequence <math>s_n^2</math> is still constant-recursive (see [[#Closure properties|closure properties]]), the existence-of-a-zero problem in the table above [[Reduction (recursion theory)|reduces to]] positivity, and infinitely-many-zeros reduces to eventual positivity. Other problems also reduce to those in the above table: for example, whether <math>s_n = c</math> for some <math>n</math> reduces to existence-of-a-zero for the sequence <math>s_n - c</math>. As a second example, for sequences in the real numbers, ''weak'' positivity (is <math>s_n \ge 0</math> for all <math>n</math>?) reduces to positivity of the sequence <math>-s_n</math> (because the answer must be negated, this is a [[Turing reduction]]). |
|||
that is, time-shifted version of eigenvector,''e'', has components ''λ'' times larger, the eigenvector components are powers of ''λ'', <math>\vec e_i = \begin{bmatrix}\lambda_i^{n-1} & \cdots & \lambda_i^2 & \lambda_i & 1\end{bmatrix}^T,</math> and, thus, recurrent homogeneous linear equation solution is a combination of exponential functions, <math>\vec y_n = \sum_1^n {c_i\,\lambda_i^n\,\vec e_i}</math>. The components <math>c_i</math> can be determined out of initial conditions: |
|||
The Skolem-Mahler-Lech theorem would provide answers to some of these questions, except that its proof is [[Constructive proof|non-constructive]]. It states that for all <math>n > M</math>, the zeros are repeating; however, the value of <math>M</math> is not known to be computable, so this does not lead to a solution to the existence-of-a-zero problem.<ref name="ow"/> On the other hand, the exact pattern which repeats after <math>n > M</math> ''is'' computable.<ref name="ow"/><ref>{{Cite journal|last1=Berstel|first1=Jean|last2=Mignotte|first2=Maurice|date=1976|title=Deux propriétés décidables des suites récurrentes linéaires|journal=Bulletin de la Société Mathématique de France|language=fr|volume=104|pages=175–184|doi=10.24033/bsmf.1823|doi-access=free}}</ref> This is why the infinitely-many-zeros problem is decidable: just determine if the infinitely-repeating pattern is empty. |
|||
:<math>\vec y_0 = \begin{bmatrix}y_{0}\\ y_{-1} \\ \vdots\\ y_{-n+1}\end{bmatrix} = \sum_{i=1}^n {c_i\,\lambda_i^0\,\vec e_i} = \begin{bmatrix}\vec e_1 & \vec e_2 & \cdots & \vec e_n\end{bmatrix}\,\begin{bmatrix}c_1 \\ c_2 \\ \cdots \\ c_n\end{bmatrix} = E\, \begin{bmatrix}c_1 \\ c_2 \\ \cdots \\ c_n\end{bmatrix}</math> |
|||
Decidability results are known when the order of a sequence is restricted to be small. For example, the Skolem problem is decidable for sequences of order up to 4,<ref name="ow" /> and for a restricted set of sequences up to order 7.<ref name=LICS22/> |
|||
Solving for coefficients, |
|||
==Generalizations== |
|||
:<math>\begin{bmatrix}c_1 \\ c_2 \\ \cdots \\ c_n\end{bmatrix} = E^{-1} \vec y_0 = \begin{bmatrix}\lambda_1^{n-1} & \lambda_2^{n-1} & \cdots & \lambda_n^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda_1 & \lambda_2 & \cdots & \lambda_n \\ 1 & 1 & \cdots & 1\end{bmatrix}^{-1}\,\begin{bmatrix}y_{0}\\ y_{-1} \\ \vdots\\ y_{-n+1}\end{bmatrix}.</math> |
|||
A '''[[holonomic function|D-finite or holonomic sequence]]''' is a natural generalization where the coefficients of the recurrence are allowed to be polynomial functions of <math>n</math> rather than constants.<ref>{{Cite journal |last=Stanley |first=Richard P |date=1980 |title=Differentiably finite power series |journal=European journal of combinatorics |volume=1 |issue=2 |pages=175–188}}</ref> |
|||
This also works with arbitrary boundary conditions <math>\underbrace{y_a, y_b, \ldots}_\text{n}</math>, not necessary the initial ones, |
|||
A '''[[k-regular sequence|<math>k</math>-regular sequence]]''' satisfies a linear recurrences with constant coefficients, but the recurrences take a different form. Rather than <math>s_n</math> being a linear combination of <math>s_m</math> for some integers <math>m</math> that are close to <math>n</math>, each term <math>s_n</math> in a <math>k</math>-regular sequence is a linear combination of <math>s_m</math> for some integers <math>m</math> whose [[radix|base]]-<math>k</math> representations are close to that of <math>n</math>.<ref>{{Cite journal |last=Allouche |first=Jean-Paul |last2=Shallit |first2=Jeffrey |date=1992 |title=The ring of k-regular sequences |journal=Theoretical Computer Science |volume=98 |issue=2 |pages=163–197}}</ref> Constant-recursive sequences can be thought of as <math>1</math>-regular sequences, where the [[unary numeral system|base-1 representation]] of <math>n</math> consists of <math>n</math> copies of the digit <math>1</math>. |
|||
:<math>\begin{bmatrix}y_a \\ y_b \\ \vdots\end{bmatrix} = \begin{bmatrix}\vec y_a[n] \\ \vec y_b[n] \\ \vdots\end{bmatrix} = \begin{bmatrix}\sum_{i=1}^n {c_i\,\lambda_i^a\,\vec e_i[n]} \\ \sum_{i=1}^n {c_i\,\lambda_i^b\,\vec e_i[n]} \\ \vdots\end{bmatrix} =\begin{bmatrix}\sum_{i=1}^n {c_i\,\lambda_i^a\,\lambda_i^{n-1}} \\ \sum_{i=1}^n {c_i\,\lambda_i^b\,\lambda_i^{n-1}} \\ \vdots\end{bmatrix} = </math> |
|||
{{cn|date=April 2024}} |
|||
==Notes== |
|||
:<math> = \begin{bmatrix}\sum {c_i\,\lambda_i^{a+n-1}} \\ \sum {c_i\,\lambda_i^{b+n-1}} \\ \vdots\end{bmatrix} = \begin{bmatrix}\lambda_1^{a+n-1} & \lambda_2^{a+n-1} & \cdots & \lambda_n^{a+n-1} \\ \lambda_1^{b+n-1} & \lambda_2^{b+n-1} & \cdots & \lambda_n^{b+n-1} \\ \vdots & \vdots & \ddots & \vdots \end{bmatrix}\,\begin{bmatrix}c_1 \\ c_2 \\ \vdots \\ c_n\end{bmatrix}.</math> |
|||
{{reflist}} |
|||
==References== |
|||
This description is really no different from general method above, however it is more succinct. It also works nicely for situations like |
|||
{{refbegin}} |
|||
:<math>\begin{cases} |
|||
* {{cite book |last=Brousseau |first=Alfred |title=Linear Recursion and Fibonacci Sequences |year=1971 |publisher=Fibonacci Association |url=https://www.fq.math.ca/linear.html }} |
|||
a_n =a_{n-1}-b_{n-1}\\ |
|||
* {{Cite book |last1=Kauers |first1=Manuel |last2=Paule |first2=Peter |title=The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates |url=https://books.google.com/books?id=BPeODAEACAAJ |date=2010 |publisher=Springer Vienna |isbn=978-3-7091-0444-6 |language=en |pages=66 }} |
|||
b_n =2a_{n-1}+b_{n-1}. |
|||
* {{cite book |last=Stanley |first=Richard P. |date=2011 |title=Enumerative Combinatorics |url=https://www.ms.uky.edu/~sohum/putnam/enu_comb_stanley.pdf |volume=1 |edition=2 |publisher=Cambridge studies in advanced mathematics}} |
|||
\end{cases} |
|||
{{refend}} |
|||
</math> |
|||
where there are several linked recurrences.<ref>{{citation|title=Discrete Algorithmic Mathematics|first1=Stephen B.|last1=Maurer|first2=Anthony|last2=Ralston|edition=2nd|publisher=A K Peters|year=1998|isbn=9781568810911|page=609}}.</ref> |
|||
===Solving with z-transforms=== |
|||
Certain difference equations - in particular, [[Z-transform#Linear constant-coefficient difference equation|linear constant coefficient]] difference equations - can be solved using [[z-transform]]s. The ''z''-transforms are a class of [[integral transform]]s that lead to more convenient algebraic manipulations and more straightforward solutions. There are cases in which obtaining a direct solution would be all but impossible, yet solving the problem via a thoughtfully chosen integral transform is straightforward. |
|||
===Theorem=== |
|||
Given a homogeneous linear recurrence relation with constant coefficients of order ''d'', let ''p''(''t'') be the [[characteristic polynomial]] (also "auxiliary polynomial") |
|||
:<math>t^d - c_1t^{d-1} - c_2t^{d-2}-\cdots-c_{d} = 0 \,</math> |
|||
such that each ''c<sub>i</sub>'' corresponds to each ''c<sub>i</sub>'' in the original recurrence relation (see the general form above). Suppose λ is a root of ''p''(''t'') having multiplicity ''r''. This is to say that (''t''−λ)<sup>''r''</sup> divides ''p''(''t''). The following two properties hold: |
|||
# Each of the ''r'' sequences <math>\lambda^n, n\lambda^n, n^2\lambda^n,\dots,n^{r-1}\lambda^n</math> satisfies the recurrence relation. |
|||
# Any sequence satisfying the recurrence relation can be written uniquely as a linear combination of solutions constructed in part 1 as ''λ'' varies over all distinct roots of ''p''(''t''). |
|||
As a result of this theorem a homogeneous linear recurrence relation with constant coefficients can be solved in the following manner: |
|||
# Find the characteristic polynomial ''p''(''t''). |
|||
# Find the roots of ''p''(''t'') counting multiplicity. |
|||
# Write ''a<sub>n</sub>'' as a linear combination of all the roots (counting multiplicity as shown in the theorem above) with unknown coefficients ''b<sub>i</sub>''. |
|||
::<math>a_n = \left (b_1\lambda_1^n + b_2n\lambda_1^n + b_3n^2\lambda_1^n+\cdots+b_r n^{r-1}\lambda_1^n \right )+\cdots+ \left (b_{d-q+1}\lambda_{*}^n + \cdots + b_{d}n^{q-1}\lambda_{*}^n \right )</math> |
|||
:This is the general solution to the original recurrence relation. (''q'' is the multiplicity of λ<sub>*</sub>) |
|||
:4. Equate each <math>a_0, a_1, \dots,a_d</math> from part 3 (plugging in ''n'' = 0, ..., ''d'' into the general solution of the recurrence relation) with the known values <math>a_0, a_1, \dots,a_d</math> from the original recurrence relation. However, the values ''a<sub>n</sub>'' from the original recurrence relation used do not usually have to be contiguous: excluding exceptional cases, just ''d'' of them are needed (i.e., for an original homogeneous linear recurrence relation of order 3 one could use the values ''a''<sub>0</sub>, ''a''<sub>1</sub>, ''a''<sub>4</sub>). This process will produce a linear system of ''d'' equations with ''d'' unknowns. Solving these equations for the unknown coefficients <math>b_1, b_2, \dots,b_d </math> of the general solution and plugging these values back into the general solution will produce the particular solution to the original recurrence relation that fits the original recurrence relation's initial conditions (as well as all subsequent values <math>a_0,a_1,a_2,\dots</math> of the original recurrence relation). |
|||
The method for solving linear [[differential equations]] is similar to the method above—the "intelligent guess" ([[ansatz]]) for linear differential equations with constant coefficients is ''e''<sup>λ''x''</sup> where λ is a complex number that is determined by substituting the guess into the differential equation. |
|||
This is not a coincidence. Considering the [[Taylor series]] of the solution to a linear differential equation: |
|||
:<math>\sum_{n=0}^\infin \frac{f^{(n)}(a)}{n!} (x-a)^n</math> |
|||
it can be seen that the coefficients of the series are given by the ''n''<sup>th</sup> derivative of ''f''(''x'') evaluated at the point ''a''. The differential equation provides a linear difference equation relating these coefficients. |
|||
This equivalence can be used to quickly solve for the recurrence relationship for the coefficients in the power series solution of a linear differential equation. |
|||
The rule of thumb (for equations in which the polynomial multiplying the first term is non-zero at zero) is that: |
|||
:<math>y^{[k]} \to f[n+k]</math> |
|||
and more generally |
|||
:<math>x^m*y^{[k]} \to n(n-1)(n-m+1)f[n+k-m]</math> |
|||
'''Example:''' The recurrence relationship for the Taylor series coefficients of the equation: |
|||
:<math> (x^2 + 3x -4)y^{[3]} -(3x+1)y^{[2]} + 2y = 0</math> |
|||
is given by |
|||
:<math> n(n-1)f[n+1] + 3nf[n+2] -4f[n+3] -3nf[n+1] -f[n+2]+ 2f[n] = 0</math> |
|||
or |
|||
:<math>-4f[n+3] +2nf[n+2] + n(n-4)f[n+1] +2f[n] = 0.</math> |
|||
This example shows how problems generally solved using the power series solution method taught in normal differential equation classes can be solved in a much easier way. |
|||
'''Example:''' The differential equation |
|||
:<math>ay'' + by' +cy = 0</math> |
|||
has solution |
|||
:<math> y=e^{ax}.</math> |
|||
The conversion of the differential equation to a difference equation of the Taylor coefficients is |
|||
:<math>af[n + 2] + bf[n + 1] + cf[n] = 0.</math> |
|||
It is easy to see that the ''n''th derivative of ''e''<sup>''ax''</sup> evaluated at 0 is ''a''<sup>''n''</sup> |
|||
==Non-homogeneous linear recurrence relations with constant coefficients== |
|||
If the recurrence is non-homogeneous, a particular solution can be found by the [[method of undetermined coefficients]] and the solution is the sum of the solution of the homogeneous and the particular solutions. Another method to solve an non-homogeneous recurrence is the method of ''symbolic differentiation''. For example, consider the following recurrence: |
|||
:<math>a_{n+1} = a_{n} + 1</math> |
|||
This is an non-homogeneous recurrence. If we substitute ''n'' ↦ ''n''+1, we obtain the recurrence |
|||
:<math>a_{n+2} = a_{n+1} + 1</math> |
|||
Subtracting the original recurrence from this equation yields |
|||
:<math>a_{n+2} - a_{n+1} = a_{n+1} - a_n</math> |
|||
or equivalently |
|||
:<math>a_{n+2} = 2 a_{n+1} - a_n</math> |
|||
This is a homogeneous recurrence, which can be solved by the methods explained above. In general, if a linear recurrence has the form |
|||
:<math> a_{n+k} = \lambda_{k-1} a_{n+k-1} + \lambda_{k-2} a_{n+k-2} + \cdots + \lambda_1 a_{n+1} + \lambda_0 a_{n} + p(n) </math> |
|||
where <math>\lambda_0, \lambda_1, \dots, \lambda_{k-1}</math> are constant coefficients and ''p''(''n'') is the inhomogeneity, then if ''p''(''n'') is a polynomial with degree ''r'', then this non-homogeneous recurrence can be reduced to a homogeneous recurrence by applying the method of symbolic differencing ''r'' times. |
|||
If |
|||
:<math>P(x) = \sum_{n=0}^\infty p_n x^n</math> |
|||
is the generating function of the inhomogeneity, the generating function |
|||
:<math>A(x) = \sum_{n=0}^\infty a(n) x^n</math> |
|||
of the non-homogeneous recurrence |
|||
:<math> a_n = \sum_{i=1}^s c_i a_{n-i}+p_n,\quad n\ge n_r,</math> |
|||
with constant coefficients {{math|c<sub>i</sub>}} is derived from |
|||
:<math> \left (1-\sum_{i=1}^sc_ix^i \right )A(x)=P(x)+\sum_{n=0}^{n_r-1}[a_n-p_n]x^n-\sum_{i=1}^s c_ix^i\sum_{n=0}^{n_r-i-1}a_nx^n.</math> |
|||
If ''P''(''x'') is a rational generating function, ''A''(''x'') is also one. The case discussed above, where ''p<sub>n</sub>'' = ''K'' is a constant, emerges as one example of this formula, with ''P''(''x'') = ''K''/(1−''x''). Another example, the recurrence <math>a_n=10 a_{n-1}+n</math> with linear inhomogeneity, arises in the definition of the [[schizophrenic number]]s. The solution of homogeneous recurrences is incorporated as ''p'' = ''P'' = 0. |
|||
== Notes == |
|||
{{reflist}} |
|||
[[Category:Combinatorics]] |
|||
== References == |
|||
[[Category:Dynamical systems]] |
|||
* {{cite book| first1=Alfred | last1=Brousseau |
|||
[[Category:Integer sequences]] |
|||
|title=Linear Recursion and Fibonacci Sequences |
|||
[[Category:Linear algebra]] |
|||
|year=1971 |
|||
[[Category:Recurrence relations]] |
|||
|publisher=Fibonacci Association |
|||
|url=http://www.fq.math.ca/linear.html |
|||
}} |
|||
*{{cite book| first1=Ronald L. | last1=Graham | |
|||
first2=Donald E. | last2=Knuth |
|||
|first3=Oren | last3=Patashnik |
|||
|title=[[Concrete Mathematics]]: A Foundation for Computer Science |
|||
|edition=2 |
|||
|publisher=Addison-Welsey |
|||
|year=1994 |isbn=0-201-55802-5 |
|||
}} |
|||
== |
==External links== |
||
* {{cite web |title= OEIS Index Rec|url=http://oeis.org/wiki/Index_to_OEIS:_Section_Rec}} [[OEIS]] index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients) |
* {{cite web |title= OEIS Index Rec|url=http://oeis.org/wiki/Index_to_OEIS:_Section_Rec}} [[On-Line Encyclopedia of Integer Sequences|OEIS]] index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients) |
||
Revision as of 03:54, 19 April 2024
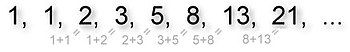

In mathematics, an infinite sequence of numbers is called constant-recursive if it satisfies an equation of the form
for all , where are constants. The equation is called a linear recurrence relation. The concept is also known as a linear recurrence sequence, linear-recursive sequence, linear-recurrent sequence, or a C-finite sequence.[1]
For example, the Fibonacci sequence
- ,
is constant-recursive because it satisfies the linear recurrence : each number in the sequence is the sum of the previous two.[2] Other examples include the power of two sequence , where each number is the sum of twice the previous number, and the square number sequence . All arithmetic progressions, all geometric progressions, and all polynomials are constant-recursive. However, not all sequences are constant-recursive; for example, the factorial sequence is not constant-recursive.
Constant-recursive sequences are studied in combinatorics and the theory of finite differences. They also arise in algebraic number theory, due to the relation of the sequence to polynomial roots; in the analysis of algorithms, as the running time of simple recursive functions; and in the theory of formal languages, where they count strings up to a given length in a regular language. Constant-recursive sequences are closed under important mathematical operations such as term-wise addition, term-wise multiplication, and Cauchy product.
The Skolem–Mahler–Lech theorem states that the zeros of a constant-recursive sequence have a regularly repeating (eventually periodic) form. The Skolem problem, which asks for an algorithm to determine whether a linear recurrence has at least one zero, is an unsolved problem in mathematics.
Definition
A constant-recursive sequence is any sequence of integers, rational numbers, algebraic numbers, real numbers, or complex numbers (written as as a shorthand) satisfying a formula of the form
for all for some fixed coefficients ranging over the same domain as the sequence (integers, rational numbers, algebraic numbers, real numbers, or complex numbers). The equation is called a linear recurrence with constant coefficients of order d. The order of the sequence is the smallest positive integer such that the sequence satisfies a recurrence of order d, or for the everywhere-zero sequence.[citation needed]
The definition above allows eventually-periodic sequences such as and . Some authors require that , which excludes such sequences.[3][4][5]
Examples
| Name | Order ( ) | First few values | Recurrence (for ) | Generating function | OEIS |
|---|---|---|---|---|---|
| Zero sequence | 0 | 0, 0, 0, 0, 0, 0, ... | A000004 | ||
| One sequence | 1 | 1, 1, 1, 1, 1, 1, ... | A000012 | ||
| Characteristic function of | 1 | 1, 0, 0, 0, 0, 0, ... | A000007 | ||
| Powers of two | 1 | 1, 2, 4, 8, 16, 32, ... | A000079 | ||
| Powers of −1 | 1 | 1, −1, 1, −1, 1, −1, ... | A033999 | ||
| Characteristic function of | 2 | 0, 1, 0, 0, 0, 0, ... | A063524 | ||
| Decimal expansion of 1/6 | 2 | 1, 6, 6, 6, 6, 6, ... | A020793 | ||
| Decimal expansion of 1/11 | 2 | 0, 9, 0, 9, 0, 9, ... | A010680 | ||
| Nonnegative integers | 2 | 0, 1, 2, 3, 4, 5, ... | A001477 | ||
| Odd positive integers | 2 | 1, 3, 5, 7, 9, 11, ... | A005408 | ||
| Fibonacci numbers | 2 | 0, 1, 1, 2, 3, 5, 8, 13, ... | A000045 | ||
| Lucas numbers | 2 | 2, 1, 3, 4, 7, 11, 18, 29, ... | A000032 | ||
| Pell numbers | 2 | 0, 1, 2, 5, 12, 29, 70, ... | A000129 | ||
| Powers of two interleaved with 0s | 2 | 1, 0, 2, 0, 4, 0, 8, 0, ... | A077957 | ||
| Inverse of 6th cyclotomic polynomial | 2 | 1, 1, 0, −1, −1, 0, 1, 1, ... | A010892 | ||
| Triangular numbers | 3 | 0, 1, 3, 6, 10, 15, 21, ... | A000217 |
Fibonacci and Lucas sequences
The sequence 0, 1, 1, 2, 3, 5, 8, 13, ... of Fibonacci numbers is constant-recursive of order 2 because it satisfies the recurrence with . For example, and . The sequence 2, 1, 3, 4, 7, 11, ... of Lucas numbers satisfies the same recurrence as the Fibonacci sequence but with initial conditions and . More generally, every Lucas sequence is constant-recursive of order 2.[2]
Arithmetic progressions
For any and any , the arithmetic progression is constant-recursive of order 2, because it satisfies . Generalizing this, see polynomial sequences below.[citation needed]
Geometric progressions
For any and , the geometric progression is constant-recursive of order 1, because it satisfies . This includes, for example, the sequence 1, 2, 4, 8, 16, ... as well as the rational number sequence .[citation needed]
Eventually periodic sequences
A sequence that is eventually periodic with period length is constant-recursive, since it satisfies for all , where the order is the length of the initial segment including the first repeating block. Examples of such sequences are 1, 0, 0, 0, ... (order 1) and 1, 6, 6, 6, ... (order 2).[citation needed]
Polynomial sequences
A sequence defined by a polynomial is constant-recursive. The sequence satisfies a recurrence of order (where is the degree of the polynomial), with coefficients given by the corresponding element of the binomial transform.[7][8] The first few such equations are
- for a degree 0 (that is, constant) polynomial,
- for a degree 1 or less polynomial,
- for a degree 2 or less polynomial, and
- for a degree 3 or less polynomial.
A sequence obeying the order-d equation also obeys all higher order equations. These identities may be proved in a number of ways, including via the theory of finite differences.[9] Any sequence of integer, real, or complex values can be used as initial conditions for a constant-recursive sequence of order . If the initial conditions lie on a polynomial of degree or less, then the constant-recursive sequence also obeys a lower order equation.
Enumeration of words in a regular language
Let be a regular language, and let be the number of words of length in . Then is constant-recursive.[10] For example, for the language of all binary strings, for the language of all unary strings, and for the language of all binary strings that do not have two consecutive ones. More generally, any function accepted by a weighted automaton over the unary alphabet over the semiring (which is in fact a ring, and even a field) is constant-recursive.[citation needed]
Other examples
The sequences of Jacobsthal numbers, Padovan numbers, Pell numbers, and Perrin numbers[2] are constant-recursive.
Non-examples
The factorial sequence is not constant-recursive. More generally, every constant-recursive function is asymptotically bounded by an exponential function (see #Closed-form characterization) and the factorial sequence grows faster than this.
The Catalan sequence is not constant-recursive. This is because the generating function of the Catalan numbers is not a rational function (see #Equivalent definitions).
Equivalent definitions
In terms of matrices
A sequence is constant-recursive of order less than or equal to if and only if it can be written as
where is a vector, is a matrix, and is a vector, where the elements come from the same domain (integers, rational numbers, algebraic numbers, real numbers, or complex numbers) as the original sequence. Specifically, can be taken to be the first values of the sequence, the linear transformation that computes from , and the vector .[11]
In terms of non-homogeneous linear recurrences
| Non-homogeneous | Homogeneous |
|---|---|
A non-homogeneous linear recurrence is an equation of the form
where is an additional constant. Any sequence satisfying a non-homogeneous linear recurrence is constant-recursive. This is because subtracting the equation for from the equation for yields a homogeneous recurrence for , from which we can solve for to obtain[citation needed]
In terms of generating functions
A sequence is constant-recursive precisely when its generating function
is a rational function , where and are polynomials and .[3] Moreover, the order of the sequence is the minimum such that it has such a form with and .[12]
The denominator is the polynomial obtained from the auxiliary polynomial by reversing the order of the coefficients, and the numerator is determined by the initial values of the sequence:[13][14]
where
It follows from the above that the denominator must be a polynomial not divisible by (and in particular nonzero).
In terms of sequence spaces
A sequence is constant-recursive if and only if the set of sequences
is contained in a sequence space (vector space of sequences) whose dimension is finite. That is, is contained in a finite-dimensional subspace of closed under the left-shift operator.[16][17]
This characterization is because the order- linear recurrence relation can be understood as a proof of linear dependence between the sequences for . An extension of this argument shows that the order of the sequence is equal to the dimension of the sequence space generated by for all .[18][17]
Closed-form characterization
Constant-recursive sequences admit the following unique closed form characterization using exponential polynomials: every constant-recursive sequence can be written in the form
for all , where
- The term is a sequence which is zero for all (where is the order of the sequence);
- The terms are complex polynomials; and
- The terms are distinct complex constants.[19][3]
This characterization is exact: every sequence of complex numbers that can be written in the above form is constant-recursive.[20]
For example, the Fibonacci number is written in this form using Binet's formula:[21]
where is the golden ratio and . These are the roots of the equation . In this case, , for all , are both constant polynomials, , and .
The term is only needed when ; if then it corrects for the fact that some initial values may be exceptions to the general recurrence. In particular, for all .[citation needed]
The complex numbers are the roots of the characteristic polynomial of the recurrence:
whose coefficients are the same as those of the recurrence.[22] If the sequence consists of integers or rational numbers, the roots will be algebraic numbers. If the roots are all distinct, then the polynomials are all constants, which can be determined from the initial values of the sequence. If the roots of the characteristic polynomial are not distinct, and is a root of multiplicity , then in the formula has degree . For instance, if the characteristic polynomial factors as , with the same root r occurring three times, then the th term is of the form [23][24]
Closure properties
Examples
The sum of two constant-recursive sequences is also constant-recursive.[25][26] For example, the sum of and is (), which satisfies the recurrence . The new recurrence can be found by adding the generating functions for each sequence.
Similarly, the product of two constant-recursive sequences is constant-recursive.[25] For example, the product of and is (), which satisfies the recurrence .
The left-shift sequence and the right-shift sequence (with ) are constant-recursive because they satisfy the same recurrence relation. For example, because is constant-recursive, so is .
List of operations
In general, constant-recursive sequences are closed under the following operations, where denote constant-recursive sequences, are their generating functions, and are their orders, respectively.[27]
| Operation | Definition | Requirement | Generating function equivalent | Order |
|---|---|---|---|---|
| Term-wise sum | — | [25] | ||
| Term-wise product | — | [28][29] | [11][25] | |
| Cauchy product | — | [27] | ||
| Left shift | — | [27] | ||
| Right shift | — | [27] | ||
| Cauchy inverse | [27] | |||
| Kleene star | [27] |
The closure under term-wise addition and multiplication follows from the closed-form characterization in terms of exponential polynomials. The closure under Cauchy product follows from the generating function characterization.[27] The requirement for Cauchy inverse is necessary for the case of integer sequences, but can be replaced by if the sequence is over any field (rational, algebraic, real, or complex numbers).[27]
Behavior
Is there an algorithm to test whether a constant-recursive sequence has a zero?
Zeros
Despite satisfying a simple local formula, a constant-recursive sequence can exhibit complicated global behavior. Define a zero of a constant-recursive sequence to be a nonnegative integer such that . The Skolem–Mahler–Lech theorem states that the zeros of the sequence are eventually repeating: there exists constants and such that for all , if and only if . This result holds for a constant-recursive sequence over the complex numbers, or more generally, over any field of characteristic zero.[30]
Decision problems
The pattern of zeros in a constant-recursive sequence can also be investigated from the perspective of computability theory. To do so, the description of the sequence must be given a finite description; this can be done if the sequence is over the integers or rational numbers, or even over the algebraic numbers.[11] Given such an encoding for sequences , the following problems can be studied:
| Problem | Description | Status[11][31] |
|---|---|---|
| Existence of a zero (Skolem problem) | On input , is for some ? | Open |
| Infinitely many zeros | On input , is for infinitely many ? | Decidable |
| Eventually all zero | On input , is for all sufficiently large ? | Decidable |
| Positivity | On input , is for all ? | Open |
| Eventual positivity | On input , is for all sufficiently large ? | Open |
Because the square of a constant-recursive sequence is still constant-recursive (see closure properties), the existence-of-a-zero problem in the table above reduces to positivity, and infinitely-many-zeros reduces to eventual positivity. Other problems also reduce to those in the above table: for example, whether for some reduces to existence-of-a-zero for the sequence . As a second example, for sequences in the real numbers, weak positivity (is for all ?) reduces to positivity of the sequence (because the answer must be negated, this is a Turing reduction).
The Skolem-Mahler-Lech theorem would provide answers to some of these questions, except that its proof is non-constructive. It states that for all , the zeros are repeating; however, the value of is not known to be computable, so this does not lead to a solution to the existence-of-a-zero problem.[11] On the other hand, the exact pattern which repeats after is computable.[11][32] This is why the infinitely-many-zeros problem is decidable: just determine if the infinitely-repeating pattern is empty.
Decidability results are known when the order of a sequence is restricted to be small. For example, the Skolem problem is decidable for sequences of order up to 4,[11] and for a restricted set of sequences up to order 7.[31]
Generalizations
A D-finite or holonomic sequence is a natural generalization where the coefficients of the recurrence are allowed to be polynomial functions of rather than constants.[33]
A -regular sequence satisfies a linear recurrences with constant coefficients, but the recurrences take a different form. Rather than being a linear combination of for some integers that are close to , each term in a -regular sequence is a linear combination of for some integers whose base- representations are close to that of .[34] Constant-recursive sequences can be thought of as -regular sequences, where the base-1 representation of consists of copies of the digit .[citation needed]
Notes
- ^ Kauers & Paule 2010, p. 63.
- ^ a b c Kauers & Paule 2010, p. 70.
- ^ a b c Stanley 2011, p. 464.
- ^ Kauers & Paule 2010, p. 66.
- ^ Halava, Vesa; Harju, Tero; Hirvensalo, Mika; Karhumäki, Juhani (2005), Skolem's Problem – On the Border between Decidability and Undecidability, p. 1, CiteSeerX 10.1.1.155.2606
- ^ "Index to OEIS: Section Rec - OeisWiki". oeis.org. Retrieved 2024-04-18.
- ^ Boyadzhiev, Boyad (2012). "Close Encounters with the Stirling Numbers of the Second Kind" (PDF). Math. Mag. 85 (4): 252–266. arXiv:1806.09468. doi:10.4169/math.mag.85.4.252. S2CID 115176876.
- ^ Riordan, John (1964). "Inverse Relations and Combinatorial Identities". The American Mathematical Monthly. 71 (5): 485–498. doi:10.1080/00029890.1964.11992269. ISSN 0002-9890.
- ^ Jordan, Charles; Jordán, Károly (1965). Calculus of Finite Differences. American Mathematical Soc. pp. 9–11. ISBN 978-0-8284-0033-6. See formula on p.9, top.
- ^ Kauers & Paule 2010, p. 81.
- ^ a b c d e f g Ouaknine, Joël; Worrell, James (2012), "Decision problems for linear recurrence sequences", Reachability Problems: 6th International Workshop, RP 2012, Bordeaux, France, September 17–19, 2012, Proceedings, Lecture Notes in Computer Science, vol. 7550, Heidelberg: Springer-Verlag, pp. 21–28, doi:10.1007/978-3-642-33512-9_3, ISBN 978-3-642-33511-2, MR 3040104.
- ^ Stanley 2011, pp. 464–465.
- ^ Martino, Ivan; Martino, Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum. 88 (3): 569–574. arXiv:1207.0111. doi:10.1007/s00233-013-9551-2. ISSN 0037-1912. S2CID 119625519.
- ^ Kauers & Paule 2010, p. 74.
- ^ Stanley 2011, pp. 468–469.
- ^ Kauers & Paule 2010, p. 67.
- ^ a b Stanley 2011, p. 465.
- ^ Kauers & Paule 2010, p. 69.
- ^ Brousseau 1971, pp. 28–34, Lesson 5.
- ^ Kauers & Paule 2010, pp. 68–70.
- ^ Brousseau 1971, p. 16, Lesson 3.
- ^ Brousseau 1971, p. 28, Lesson 5.
- ^ Greene, Daniel H.; Knuth, Donald E. (1982), "2.1.1 Constant coefficients – A) Homogeneous equations", Mathematics for the Analysis of Algorithms (2nd ed.), Birkhäuser, p. 17.
- ^ Brousseau 1971, pp. 29–31, Lesson 5.
- ^ a b c d Kauers & Paule 2010, p. 71.
- ^ Brousseau 1971, p. 37, Lesson 6.
- ^ a b c d e f g h Stanley 2011, pp. 471.
- ^ Pohlen, Timo (2009). "The Hadamard product and universal power series" (PDF). University of Trier (Doctoral Dissertation): 36–37.
- ^ See Hadamard product (series) and Parseval's theorem.
- ^ Lech, C. (1953), "A Note on Recurring Series", Arkiv för Matematik, 2 (5): 417–421, Bibcode:1953ArM.....2..417L, doi:10.1007/bf02590997
- ^ a b Lipton, Richard; Luca, Florian; Nieuwveld, Joris; Ouaknine, Joël; Purser, David; Worrell, James (2022-08-04). "On the Skolem Problem and the Skolem Conjecture". Proceedings of the 37th Annual ACM/IEEE Symposium on Logic in Computer Science. LICS '22. New York, NY, USA: Association for Computing Machinery. pp. 1–9. doi:10.1145/3531130.3533328. ISBN 978-1-4503-9351-5.
- ^ Berstel, Jean; Mignotte, Maurice (1976). "Deux propriétés décidables des suites récurrentes linéaires". Bulletin de la Société Mathématique de France (in French). 104: 175–184. doi:10.24033/bsmf.1823.
- ^ Stanley, Richard P (1980). "Differentiably finite power series". European journal of combinatorics. 1 (2): 175–188.
- ^ Allouche, Jean-Paul; Shallit, Jeffrey (1992). "The ring of k-regular sequences". Theoretical Computer Science. 98 (2): 163–197.
References
- Brousseau, Alfred (1971). Linear Recursion and Fibonacci Sequences. Fibonacci Association.
- Kauers, Manuel; Paule, Peter (2010). The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates. Springer Vienna. p. 66. ISBN 978-3-7091-0444-6.
- Stanley, Richard P. (2011). Enumerative Combinatorics (PDF). Vol. 1 (2 ed.). Cambridge studies in advanced mathematics.
External links
- "OEIS Index Rec". OEIS index to a few thousand examples of linear recurrences, sorted by order (number of terms) and signature (vector of values of the constant coefficients)
























































































![{\displaystyle [0,0,\ldots ,0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604c5e8eaed13f4c3805ebb80b68d31635175be6)









































































































