→Empty function: "category of sets" is the correct name - functions are morphisms in this category |
→Introduction and examples: rm section: there are more significant examples in the lead and in other sections. For these trivial examples the figures give sufficient information |
||
| (79 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Function machine2.svg|thumb|right|A function ''f'' takes an input ''x'', and returns a single output ''f''(''x''). One metaphor describes the function as a "machine" or "[[black box]]" that for each input returns a corresponding output.]] |
|||
[[Image:Graph of example function.svg|thumb|250px|The red curve is the [[graph of a function]] ''f'' in the [[Cartesian plane]], consisting of all points with coordinates of the form {{nowrap|(''x'', ''f''(''x''))}}. The property of having one output for each input is represented geometrically by the fact that [[Vertical line test|each vertical line]] (such as the yellow line through the origin) has exactly one crossing point with the curve.]] |
|||
{{Functions}} |
{{Functions}} |
||
In [[mathematics]], a '''function'''<ref>The words '''map''' or '''mapping''', '''[[Transformation (function)|transformation]]''', '''correspondence''', and '''operator''' are often used synonymously. {{harvnb |Halmos |1970 |p=30}}.</ref> is |
In [[mathematics]], a '''function'''<ref>The words '''map''' or '''mapping''', '''[[Transformation (function)|transformation]]''', '''correspondence''', and '''operator''' are often used synonymously. {{harvnb |Halmos |1970 |p=30}}.</ref> is originally the idealization of how a varying quantity depends on another quantity. For example, the position of a [[planet]] is a ''function'' of the time. [[History of the function concept|Historically]], the concept was elaborated with the [[infinitesimal calculus]] at the end of 17th century, and, until the 19th century, the function that were considered were [[differentiable function|differentiable]] (that is they have a high degree of regularity). The concept of function has been formalized at the end of the 19th century in terms of [[set theory]], and this has much enlarged the domains of application of the concept. |
||
A function is a process or a relation<!-- Please, do not link to [[Binary relation]], this is not the technical meaning that is intended--> that associates each element {{mvar|x}} of a [[set (mathematics)|set]] {{mvar|X}}, the ''domain'' of the function, to a unique element {{mvar|y}} of another set {{mvar|Y}} (possibly the same set), the ''codomain'' of the function. If the function is called {{mvar|f}}, this relation is denoted {{math|1=''y'' = ''f''{{space|hair}}(''x'')}} (read {{mvar|f}} of {{mvar|x}}), the element {{mvar|x}} is the ''argument'' or ''input'' of the function, and {{mvar|y}} is the ''value of the function'', the ''output'', or the ''image'' of {{mvar|x}} by {{mvar|f}}. The symbol that is used for representing the input is the [[variable (mathematics)|variable]] of the function (one says often that {{mvar|f}} is a function of the variable {{mvar|x}}).<ref name=MacLane>{{cite book | last = MacLane | first = Saunders | authorlink = Saunders MacLane | last2 = Birkhoff | first2 = Garrett | author2-link = Garrett Birkhoff | title = Algebra | publisher = Macmillan | edition = First | year = 1967 | location = New York | pages = 1–13 }}</ref> |
|||
Functions of various kinds are "the central objects of investigation"{{sfn |Spivak |2008 |p=39}} in most fields of modern [[mathematics]]. There are many ways to describe or represent a function. Some functions may be defined by a [[formula]] or [[algorithm]] that tells how to compute the output for a given input. A picture, with some input, output pairs shown on [[Cartesian coordinate system|Cartesian coordinates]], is called the [[graph of a function|graph of the function]], and may give an intuitive idea of some of the main features of the function, for example its maximums and minimums. In science, functions are sometimes defined by a table that gives the outputs for selected inputs. In this case, if there is reason to believe the function is [[smooth function|smooth]], it is sometimes assumed that the values in between the points on the table also exist, but are not known with the accuracy of the measured points. For example, a table might give the temperature at a particular place at specified times, with the assumption that the temperature is a smooth function of time, even though the temperature at times other than those measured is not known. Another form in which functions are given is the [[implicit function]], for example as an [[inverse function|inverse]] to another function or as a solution of a [[differential equation]]. |
|||
A function is uniquely represented by its [[graph of a function|graph]] which is the set of all [[pair (mathematics)|pairs]] {{math|(''x'', ''f''{{space|hair}}(''x''))}}. When the domain and the codomain are sets of [[number]]s, each such pair may be considered as the [[Cartesian coordinates]] of a point in the plane. In general, these points form a curve, which is also called the graph of the function. This is a useful representation of the function, which is commonly used everywhere, for example in newspapers. |
|||
In modern mathematics,<ref name=MacLane>{{cite book | last = MacLane | first = Saunders | authorlink = Saunders MacLane | last2 = Birkhoff | first2 = Garrett | author2-link = Garrett Birkhoff | title = Algebra | publisher = Macmillan | edition = First | year = 1967 | location = New York | pages = 1–13 }}</ref> a function is defined by its set of inputs, called the ''[[Domain of a function|domain]]''; a set containing the set of outputs, and possibly additional elements, as members, called its ''[[codomain (mathematics)|codomain]]'' (or ''target''); and the set of all input-output pairs, called its ''[[graph of a function|graph]]''. Sometimes the codomain is called the function's "range", but more commonly the word "range" is used to mean, instead, specifically the set of outputs (this is also called the ''[[Image (mathematics)|image]]'' of the function). For example, we could define a function using the rule {{nowrap|1=''f''(''x'') = ''x''<sup>2</sup>}} by saying that the domain and codomain are the [[real numbers]], and that the graph consists of all pairs of real numbers {{nowrap|1=(''x'', ''x''<sup>2</sup>)}}. The image of this function is the set of non-negative real numbers. Collections of functions with the same domain and the same codomain are called [[function space]]s, the properties of which are studied in such mathematical disciplines as [[real analysis]], [[complex analysis]], and [[functional analysis]]. |
|||
Functions are widely used in [[science]], and in most fields of mathematics. Their role is so important that it has been said the they are "the central objects of investigation" in most fields of mathematics.{{sfn |Spivak |2008 |p=39}} |
|||
In analogy with [[arithmetic]], it is possible to define addition, subtraction, multiplication, and division of functions, in those cases where the output is a number. Another important operation defined on functions is [[composition of functions|function composition]], where the output from one function becomes the input to another function. |
|||
[[File:Function machine2.svg|thumb|right|Metaphor describing a function as a "machine" or "[[black box]]" that for each input returns a corresponding output.]] |
|||
[[Image:Graph of example function.svg|thumb|right|The red curve is the [[graph of a function]], because any [[Vertical line test|vertical line]] has exactly one crossing point with the curve.]] |
|||
==Introduction and examples== |
|||
[[File:Function color example 3.svg|thumb|A function that associates any of the four colored shapes to its color.]] |
[[File:Function color example 3.svg|thumb|A function that associates any of the four colored shapes to its color.]] |
||
For an example of a function, let ''X'' be the [[set (mathematics)|set]] consisting of four shapes: a red triangle, a yellow rectangle, a green hexagon, and a red square; and let ''Y'' be the set consisting of five colors: red, blue, green, pink, and yellow. Linking each shape to its color is a function from ''X'' to ''Y'': each shape is linked to a color (i.e., an element in ''Y''), and each shape is "linked", or "mapped", to exactly one color. There is no shape that lacks a color and no shape that has more than one color. This function will be referred to as the "color-of-the-shape function". |
|||
The input to a function is called the [[Argument of a function|argument]] and the output is called the [[Value (mathematics)|value]]. The set of all permitted inputs to a given function is called the [[domain of a function|domain]] of the function, while the set of permissible outputs is called the [[codomain]]. Thus, the domain of the "color-of-the-shape function" is the set of the four shapes, and the codomain consists of the five colors. The concept of a function does ''not'' require that every possible output is the value of some argument, e.g. the color blue is not the color of any of the four shapes in ''X''. |
|||
A second example of a function is the following: the domain is chosen to be the set of [[natural numbers]] (1, 2, 3, 4, ...), and the codomain is the set of [[integer]]s (..., −3, −2, −1, 0, 1, 2, 3, ...). The function associates to any natural number ''n'' the number 4−''n''. For example, to 1 it associates 3 and to 10 it associates −6. |
|||
A third example of a function has the set of [[polygon]]s as domain and the set of natural numbers as codomain. The function associates a polygon with its number of [[vertex (geometry)|vertices]]. For example, a triangle is associated with the number 3, a square with the number 4, and so on. |
|||
The term [[range (mathematics)|range]] is sometimes used either for the codomain or for the set of all the actual values a function has. |
|||
==Definition== |
==Definition== |
||
| Line 34: | Line 25: | ||
| caption2 = However, this second diagram does ''not'' represent a function. One reason is that 2 is the first element in more than one ordered pair. In particular, {{nowrap|(2, B)}} and {{nowrap|(2, C)}} are both elements of the set of ordered pairs. Another reason, sufficient by itself, is that 3 is not the first element (input) for any ordered pair. A third reason, likewise, is that 4 is not the first element of any ordered pair. |
| caption2 = However, this second diagram does ''not'' represent a function. One reason is that 2 is the first element in more than one ordered pair. In particular, {{nowrap|(2, B)}} and {{nowrap|(2, C)}} are both elements of the set of ordered pairs. Another reason, sufficient by itself, is that 3 is not the first element (input) for any ordered pair. A third reason, likewise, is that 4 is not the first element of any ordered pair. |
||
}} |
}} |
||
When students first begin to study functions, intuitive ideas such as "rules" and "associates" are used. In more advanced mathematics, more precise definitions are needed. The precise mathematical definition of a function relies on the notion of an [[ordered pair]]. |
|||
In order to avoid the use of the informally defined concepts of "rules" and "associates", the above intuitive explanation of functions is completed with a formal definition. This definition relies on the notion of the [[Cartesian product]]. The Cartesian product of two sets ''X'' and ''Y'' is the set of all [[ordered pair]]s, written (''x'', ''y''), where ''x'' is an element of ''X'' and ''y'' is an element of ''Y''. The ''x'' and the ''y'' are called the components of the ordered pair. The Cartesian product of ''X'' and ''Y'' is denoted by ''X'' × ''Y''. |
|||
A function ''f'' from ''X'' to ''Y'' is a |
A function {{math|''f''}} from {{math|''X''}} to {{math|''Y''}} is defined by a set of ordered pairs {{math|(''x'', ''y'')}} such that {{math|''x'' ∈ ''X''}} and {{math|''y'' ∈ ''Y''}}, which is subject to the following condition: every element of {{math|''X''}} is the first component of one and only one ordered pair in the set.<ref>{{cite book |last=Hamilton |first=A. G. |title=Numbers, sets, and axioms: the apparatus of mathematics |page=83 |publisher=Cambridge University Press |isbn=0-521-24509-5 |url=https://books.google.com/books?id=OXfmTHXvRXMC&pg=PA83&dq=%22function+is+a+relation%22}}</ref> In other words, for every {{math|''x''}} in {{math|''X''}} there is exactly one element {{math|''y''}} such that the ordered pair {{math|(''x'', ''y'')}} belongs to the set of pairs defining the function {{math|''f''}}. |
||
In this definition, {{math|''X''}} and {{math|''Y''}} are respectively called the ''domain'' and the ''codomain'' of the function {{mvar|f}}. If {{math|(''x'', ''y'')}} belongs to the set defining {{mvar|f}}, then {{mvar|y}} is the ''value'' of {{mvar|f}} for the ''argument'' {{mvar|x}}, or the ''image'' of {{mvar|x}} under {{mvar|f}}. One says also that {{mvar|y}} is the value of {{mvar|f}} for the ''value {{mvar|x}} of the variable''. |
|||
Considering the "color-of-the-shape" function above, the set ''X'' is the domain consisting of the four shapes, while ''Y'' is the codomain consisting of five colors. There are twenty possible ordered pairs (four shapes times five colors), one of which is |
|||
:("yellow rectangle", "red"). |
|||
The [[range (mathematics)|range]] denotes generally the image of a function, that is the set of all images of elements of the domain. However it is sometimes used as a synonym of codomain, generally in old textbooks. |
|||
The "color-of-the-shape" function described above consists of the set of those ordered pairs, |
|||
:(shape, color) |
|||
where the color is the actual color of the given shape. Thus, the pair ("red triangle", "red") is in the function, but the pair ("yellow rectangle", "red") is not. |
|||
==Notation== |
==Notation== |
||
{{see also|Functional notation}} |
{{see also|Functional notation}} |
||
A function ''f'' |
A function {{math|''f''}} with domain {{math|''X''}} and codomain {{math|''Y''}} is commonly denoted |
||
:<math>f\colon X \ |
:<math>f\colon X \to Y</math> |
||
or |
or |
||
:<math>X ~ \stackrel{f}{\ |
:<math>X ~ \stackrel{f}{\to} ~ Y.</math> |
||
In this context, the elements of ''X'' are called [[Argument of a function|arguments]] of ''f''. For each argument ''x'', the corresponding unique ''y'' in the codomain is called the function [[Value (mathematics)|value]] at ''x'' or the ''image'' of ''x'' under ''f''. It is written as ''f''(''x''). One says that ''f'' associates ''y'' with ''x'' or maps ''x'' to ''y''. This is abbreviated by |
|||
:<math>y = f(x).</math> |
|||
The notation |
|||
A general function, to be defined for a particular context, is usually denoted by a single letter, most often the lower-case letters ''f'', ''g'', ''h''. Special functions that have widely recognized names and definitions often have abbreviations, such as sin for the [[sine function]]. The value of the function ''f'' for an input ''x'' is denoted ''f''(''x''). Sometimes the parentheses are omitted if no ambiguity arises, as with ''x'' itself, but are always required if the input is, for example, a binomial such as {{nowrap|''x'' + 1.}} By convention, general functions are displayed using an italicized letter while special functions are set in roman type. |
|||
:<math>y = f(x)</math> |
|||
means that {{math|(''x'', ''y'')}} belongs to the set of pairs defining the function {{mvar|f}}. When it is needed to refer explicitly to this set of pairs, it is denoted |
|||
:<math>\{(x,f(x))\colon x\in X\}.</math> |
|||
The symbol used to denote a particular function consists generally of a single letter in [[italic font]], most often the lower-case letters {{math|''f'', ''g'', ''h''}}. Some widely used functions are represented by a symbol consisting of several letters (generally an abbreviation of their name). In this case, it is set in [[roman type]], such as "{{math|sin}}" for the [[sine function]]. |
|||
In most cases, a function is given by a formula, such as {{nowrap|1=''f''(''x'') = 2''x'' + 3,}} but in some cases, especially in advanced mathematics, it is important to also give the set of all allowable inputs, the [[domain of a function|domain]], and a set containing all outputs, the [[codomain]]. |
|||
Sometimes the parentheses of the functional notation are omitted if no ambiguity arises, as for <math>\sin x</math> instead of <math>\sin(x).</math> |
|||
The distinction between a function and its value becomes important, for instance, when one wishes to talk about the [[Duality (mathematics)|duality]] between a function and its argument. In these situations, it is desirable to show the symmetry between function and argument and place the function and the argument on an equal footing. One way to do so is to use ''bracket notation'': we write <math>[x,f]</math> for the expression ''f''(''x'').<ref>{{Cite book|url=https://archive.org/details/HalmosP.R.FiniteDimensionalVectorSpaces.SpringerVerlag205s_201703|title=Finite-Dimensional Vector Spaces|last=Halmos|first=Paul R.|publisher=Van Nostrand Company|year=1958|isbn=0-387-90093-4|location=New York|pages=21–25}}</ref> As examples, we can combine the bracket notation with the dot notation (''discussed below'') in the expression <math>[x_0,\cdot]</math> to represent the mapping (an example of a [[Linear functional|functional]]) <math>f\mapsto [x_0, f]= f(x_0)</math> for a given, fixed <math>x_0</math>, without having to introduce the letter ''f'', which is merely a placeholder ("dummy"). Although this notation might allow for cleaner expression of abstract mappings, applying it toward functions containing rational or polynomial expressions is awkward and unwieldy. Thus, this notation is seldom used in general mathematical or scientific settings. (For a related notation used in quantum mechanics, see [[bra–ket notation]].) |
|||
In many cases, a function is defined by a formula that describes how the value of the function is computed from the value of the argument. For example, if a multiplication is defined on a set {{mvar|X}}, then one may define a [[square function]] with domain and codomain {{mvar|X}} by |
|||
Practically speaking, the notation <math>\mapsto</math> ("maps to", an arrow with a bar at its tail) is flexible and convenient. It can be used to briefly mention and define a function without assigning it a name. In other cases, to define a function in full, a mapping defined with a "maps to" arrow could be stacked, in parallel, immediately below the declaration of the function name, domain, and the codomain. For example, |
|||
:<math>\ |
:<math>x\mapsto x\cdot x,</math> |
||
or, more commonly, |
|||
f\colon \mathbb{N} &\to \mathbb{Z} \\ |
|||
:<math>x\mapsto x^2.</math> |
|||
\end{align}</math> |
|||
The first part can be read as: |
|||
* "''f'' is a function from ℕ (the set of natural numbers) to ℤ (the set of integers)" or |
|||
* "''f'' is a ℤ-valued function of an ℕ-valued variable". |
|||
The second part is read: |
|||
* "''x'' maps to 4 − ''x''." |
|||
In other words, this function has the [[natural number]]s as domain, the [[integers]] as codomain. Strictly speaking, a function is properly defined only when the domain and codomain are specified. Moreover, the function |
|||
: <math>\begin{align} |
|||
g\colon \mathbb{Z} &\to \mathbb{Z} \\ |
|||
x &\mapsto 4-x. |
|||
\end{align}</math> |
|||
(with different domain) is a different function, even though the formulas defining ''f'' and ''g'' agree. Similarly, a function with a different codomain is also a different function. Nevertheless, many authors do not specify the domain and codomain, especially if these are clear from context. So in this example many just write {{nowrap|1=''f''(''x'') = 4 − ''x''}}. Sometimes, the maximal possible domain within a larger set implied by context is implicitly understood: a formula such as <math>\textstyle f(x)=\sqrt{x^2-5x+6}</math> may mean that the domain of ''f'' is the set of real numbers ''x'' where the square root is defined (in this case {{nowrap|''x'' ≤ 2}} or {{nowrap|''x'' ≥ 3}}). However, in a different context, this expression might refer to a complex-valued function <math>f:\mathbb{R}\to\mathbb{C}</math>. |
|||
Similarly, the [[identity function]] on a set {{mvar|X}} is the function |
|||
Finally, ''dot notation'' is occasionally used to specify a function by replacement of the variable of interest in an expression with a dot. For example, <math> a(\cdot)^2</math> may stand for <math> x\mapsto ax^2</math>, and <math>\textstyle \int_a^{\, (\cdot)} f(u)du</math> may stand for the integral function <math>\textstyle x\mapsto \int_a^x f(u)du</math>. |
|||
:<math>x \mapsto x.</math> |
|||
This notation {{tmath|\mapsto}} is useful for avoiding naming a function when not necessary, as in the sentence "the square function is the function <math>x \mapsto x^2.</math> |
|||
The definition of a function by a formula may use case distinction as for the definition of the [[absolute value]] of [[real number]]s: |
|||
:<math>x\mapsto |x| = \left\{ |
|||
\begin{array}{rl} |
|||
x, & \text{if } x \geq 0 \\ |
|||
-x, & \text{if } x < 0. |
|||
\end{array}\right. |
|||
</math> |
|||
Normally the definition of a function includes the definition of its domain and its codomain, but it is not always the case. Typically, a function from the reals to the reals does not always refer to a function that has the [[real number]]s a domain. This refers often to a function which has a subset of the reals as domain. In many cases some computation is needed if one want to know the domain exactly (see [[partial function]]). For example, if {{mvar|f}} is a function that has the real numbers as domain and codomain, then |
|||
<math>x\mapsto \frac 1{f(x)}</math> |
|||
is a (possibly partial) function from the reals to the reals whose domain is the set of the reals {{mvar|x}} such that {{math|''f''(''x'') ≠ 0}}. In many cases, this set is difficult to determine exactly, and often, this is not a problem for working with the function. |
|||
When the domain of a function is the set of [[natural numbers]], one talks often of a [[sequence (mathematics)]], and one uses the index notation, that is, one denotes |
|||
:<math>f_n</math> |
|||
the image of the nonnegative integer {{mvar|n}} by the function or sequence {{mvar|f}}. One says also that <math>f_n</math> is the {{mvar|n}}th element of the sequence. |
|||
Finally, ''dot notation'' is occasionally used for avoiding naming the variable. For example, <math> a(\cdot)^2</math> may stand for <math> x\mapsto ax^2</math>, and <math>\textstyle \int_a^{\, (\cdot)} f(u)du</math> may stand for the integral function <math>\textstyle x\mapsto \int_a^x f(u)du</math>. |
|||
==Specifying a function== |
==Specifying a function== |
||
In general, a specific function is defined by associating to every element of the domain a property of this element (as in the above example of colored shapes) or the result of a computation taking as input. This computation may be described by a formula. (This is the starting point of [[algebra]] of replacing many similar computations on numbers by a single formula that describes the computation on [[variable (mathematics)|variables]] representing unspecified numbers). This definition of a function uses frequently previously defined auxiliary functions. |
|||
A function can be defined by any mathematical condition relating each argument (input value) to the corresponding output value. If the domain is finite, a function ''f'' may be defined by simply tabulating all the arguments ''x'' and their corresponding function values ''f''(''x''). More commonly, a function is defined by a [[formula]], or (more generally) an [[algorithm]] — a recipe that tells how to compute the value of ''f''(''x'') given any ''x'' in the domain. |
|||
For example, the function {{mvar|f}} from the [[real number|real]]s to the reals, defined by |
|||
There are many other ways of defining functions. Examples include [[piecewise function|piecewise definitions]], [[induction (mathematics)|induction]] or [[recursion]], algebraic or [[analytic function|analytic]] [[closure (mathematics)|closure]], [[limit (mathematics)|limits]], [[analytic continuation]], infinite [[series (mathematics)|series]], and as solutions to [[integral equation|integral]] and [[differential equation]]s. The [[lambda calculus]] provides a powerful and flexible [[syntax]] for defining and combining functions of several variables. In advanced mathematics, some functions exist because of an [[axiom]], such as the [[Axiom of Choice]]. |
|||
<math>f(x)=\sqrt{1+x^2},</math> |
|||
use the [[square function]] and the [[square root function]] as auxiliary functions. The domain of {{mvar|f}} is the whole set of real numbers, even if domain of the square root function is restricted to the positive real numbers. |
|||
The computation that allows defining a function may often be described by an [[algorithm]], and any kind of algorithm may be used. Sometimes, the definition of a function may involve elements or properties that can be defined, but not computed. For example, if one, consider the set <math>\mathcal P</math> of the programs in a given programming language, which take an integer as input. The ''terminating function'' is the function that returns 1 if a progam of <math>\mathcal P</math> runs for ever when executed on a given integer input, and returns 0 otherwise. It is a basic theorem of [[computability theory]] that it cannot exist an algorithm for computing this function. |
|||
More generally, the computability theory is the study of the [[computable function]]s, that is the functions that can be computed by an algorithm. |
|||
Above ways of defining functions define them "pointwise", that is, each value is defined independently of the other values. This is not always the case. |
|||
When the domain of a function is the nonnegative integers or, more generally, when the domain may be [[well order|well ordered]], a function may be defined by [[induction (mathematics)|induction]] or [[recursion]], which means (roughly) that the definition of the function for a given input depends on previously defined values of the function. For example, the [[Fibonacci sequence]] is a function from the natural numbers into themselves that is defined by (see above for the use of indices for the argument of a function) |
|||
:<math>F_0=0, F_1=1, \text{ and } F_n=F_{n-1}+F_{n-2} \text{ for } n>1.</math> |
|||
In [[calculus]], the functions that are considered have some regularity. That is, the value of the function at a point is related with the values of the function at neighbor points. This allows defining them by [[functional equation]]s (the [[gamma function]] is the unique [[meromorphic function]] such that <math>\Gamma(z+1)=z\Gamma(z)</math> and <math>\Gamma(1)=1</math>), by [[differential equation]]s (the [[natural logarithm]] is the solution of the differential equation <math>\frac{\partial\ln x}{\partial x}=\frac 1x</math> such that {{math|1=ln(1) = 0}}), [[integral equations]] or [[analytic continuation]]. |
|||
==Representing a function== |
|||
As functions may be complicated objects, it is often useful to draw the [[graph of a function]] for getting a global view of its properties. Some functions may also represented [[histogram]]s |
|||
===Graph=== |
===Graph=== |
||
{{main|Graph of a function}} |
{{main|Graph of a function}} |
||
The ''graph'' of a function is its set of ordered pairs ''F''. This is an abstraction of the idea of a graph as a picture showing the function plotted on a pair of coordinate axes; for example, {{nowrap|(3, 9)}}, the point above 3 on the horizontal axis and to the right of 9 on the vertical axis, lies on the graph of |
|||
{{nowrap|1=''y'' = ''x''<sup>2</sup>}}. |
|||
Given a function <math>f: X\to Y,</math> its ''graph'' is, formally, the set |
|||
===Formulas and algorithms=== |
|||
Different formulas or algorithms may describe the same function. For instance {{nowrap|1=''f''(''x'') = (''x'' + 1) (''x'' − 1)}} is exactly the same function as {{nowrap|1=''f''(''x'') = ''x''<sup>2</sup> − 1}}.<ref>{{cite book |title=Theory of Recursive Functions and Effective Computation |first=Hartley|last=Rogers, Jr |authorlink=Hartley Rogers, Jr |publisher=MIT Press |pages=1–2 |year=1987 |isbn=0-262-68052-1}}</ref> |
|||
Furthermore, a function need not be described by a formula, expression, or algorithm, nor need it deal with numbers at all: the domain and codomain of a function may be arbitrary [[set (mathematics)|sets]]. One example of a function that acts on non-numeric inputs takes English words as inputs and returns the first letter of the input word as output. |
|||
:<math>G=\{(x,y): x\in X \text{ and } y=f(x)\}.</math> |
|||
As an example, the [[factorial]] function is defined on the nonnegative integers and produces a nonnegative integer. It is defined by the following inductive algorithm: 0! is defined to be 1, and ''n''! is defined to be ''n''(''n'' − 1)! for all positive integers ''n''. The factorial function is denoted with the exclamation mark (serving as the symbol of the function) after the variable ([[postfix notation]]). |
|||
In the frequent case where {{mvar|X}} and {{mvar|Y}} are subsets of the [[real number]]s (or may be identified to such subsets), an element <math>(x,y)\in G</math> may be identified with the point of coordinates {{math|''x'', ''y''}} in the [[Cartesian plane]]. Marking these points provides a drawing, generally a curve, that is also called the ''graph of the function''. For example the graph of the [[square function]] |
|||
===Computability=== |
|||
{{Main|computable function}} |
|||
Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an [[algorithm]], which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called ''[[computable function]]s''. For example, the [[Euclidean algorithm]] gives a precise process to compute the [[greatest common divisor]] of two positive integers. Many of the functions studied in the context of [[number theory]] are computable. |
|||
:<math>x\mapsto x^2</math> |
|||
Fundamental results of [[computability theory]] show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of [[cardinality]], almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is [[countable]], because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the [[real number]]s. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the [[busy beaver function]] and functions related to the [[halting problem]] and other [[List of undecidable problems|undecidable problems]]. |
|||
is a [[parabola]] that consists of all points of coordinates <math>(x, x^2)</math> for <math>x\in \R.</math> |
|||
==Basic properties== |
|||
There are a number of general basic properties and notions. In this section, ''f'' is a function with domain ''X'' and codomain ''Y''. |
|||
It is possible to draw effectively the graph of a function only if the function is sufficiently regular, that is, either if the function is [[differentiable function|differentiable]] (or [[piecewise]] differentiable) or if its domain may be identified with the integers or a subset of the integers. |
|||
===Image and preimage=== |
|||
{{Main|Image (mathematics)}} |
|||
[[File:Function image and preimage 3.png|thumb|right|The graph of the function ''f''(''x'') = ''x''<sup>3</sup> − 9''x''<sup>2</sup> + 23''x'' − 15. The [[interval (mathematics)|interval]] ''A'' = [3.5, 4.25] is a subset of the domain, thus it is shown as part of the ''x''-axis (green). The image of ''A'' is (approximately) the interval [−3.08, −1.88]. It is obtained by projecting to the ''y''-axis (along the blue arrows) the intersection of the graph with the light green area consisting of all points whose ''x''-coordinate is between 3.5 and 4.25. the part of the (vertical) ''y''-axis shown in blue. The preimage of ''B'' = [1, 2.5] consists of three intervals. They are obtained by projecting the intersection of the light red area with the graph to the ''x''-axis.]] |
|||
If ''A'' is any subset of the domain ''X'', then ''f''(''A'') is the subset of the codomain ''Y'' consisting of all images of elements of A. We say the ''f''(''A'') is the ''image'' of A under f. The ''image'' of ''f'' is given by ''f''(''X''). On the other hand, the ''[[inverse image]]'' (or ''[[preimage]]'', ''complete inverse image'') of a subset ''B'' of the codomain ''Y'' under a function ''f'' is the subset of the domain ''X'' defined by |
|||
:<math>f^{-1}(B) = \{x \in X : f(x) \in B\}.</math> |
|||
So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,2,3}. The term [[range (mathematics)|range]] usually refers to the image,<ref name="standard" /> but sometimes it refers to the codomain. |
|||
If either the domain or the codomain of the function is a subset of <math>\R^n,</math> the graph is a subset of a [[Cartesian space]] of higher dimension, and various technics have been developed for drawing it, including the use of colors for representing one of the dimensions.{{cn|date=April 2018}} |
|||
By definition of a function, the image of an element ''x'' of the domain is always a single element ''y'' of the codomain. However, the preimage of a [[Singleton (mathematics)|singleton]] set (a set with exactly one element) may in general contain any number of elements. For example, if ''f''(''x'') = 7 (the [[constant function]] taking value 7), then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. It is customary to write ''f''<sup>−1</sup>(''b'') instead of ''f''<sup>−1</sup>({''b''}), i.e. |
|||
:<math>f^{-1}(b) = \{x \in X : f(x) = b\}.</math> |
|||
This set is sometimes called the [[fiber (mathematics)|fiber]] of ''b'' under ''f''. (This notation is the same as that for the ''inverse'' ''function''. However, the inverse function <math>f^{-1}:Y\to X</math> of a function <math>f:X\to Y</math> is defined if and only if the function is ''one-to-one'' and ''onto''. ''See below of the definition of these terms.'') |
|||
===Histogram=== |
|||
Use of ''f''(''A'') to denote the image of a subset ''A'' ⊆ ''X'' is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g., in set theory, where [[Ordinal number|ordinals]] are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ''f''[''A''] for the set { ''f''(''x''): x ∈ ''A'' }. Likewise, some authors use square brackets to avoid confusion between the inverse image and the inverse function. Thus they would write ''f''<sup>−1</sup>[''B''] and ''f''<sup>−1</sup>[''b''] for the preimage of a set and a singleton. |
|||
{{main|Histogram}} |
|||
Histograms are often used for representing functions whose domain is finite, or is the [[natural number]]s or the [[integer]]s. In this case, an element {{mvar|x}} of the domain is represented by an [[interval (mathematics)|interval]] of the {{mvar|x}}-axis, and a point {{math|(''x'', ''y'')}} of the graph is represented by a [[rectangle]] with basis the interval corresponding to {{mvar|x}} and height {{mvar|y}}. |
|||
===Injective and surjective functions=== |
|||
A function is called ''[[injective function|injective]]'' (or ''one-to-one; 1-1'') if ''f''(''a'') ≠ ''f''(''b'') for any two elements ''a'', ''b'', ''a'' ≠ ''b'' of the domain. It is called ''[[surjective]]'' (or ''onto'') if the range is identical to the codomain; that is, ''f''(''X'') = ''Y''. In other words, every element ''y'' in the codomain is mapped to by ''f'' from some ''x'' in the domain. Finally ''f'' is called ''[[bijective]]'' (or the function is a ''one-to-one correspondence'') if it is both injective and surjective. A function that is injective, surjective, or bijective is referred to as an injection, a surjection, or a bijection, respectively. The existence of injections, surjections, or bijections between sets is the key concept defining the relative [[Cardinality|cardinalities]] (sizes) of the sets. |
|||
In [[statistic]], histogram are often used for representing very irregular functions. For example, for representing the function that associates his weight to each member of some population, one draws the histogram of the function that associates to each weight interval the number of people, whose weights belong to this interval. |
|||
"One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the [[Nicolas Bourbaki|Bourbaki group]] and imported into English. As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "''f'' maps ''A'' onto ''B''" differs from "''f'' maps ''A'' into ''B''" in that the former implies that ''f'' is an onto function (i.e., surjective), while the latter makes no assertion about the nature of the mapping. In more complicated statements the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms. |
|||
There are many variants of this method, see [[Histogram]] for details. |
|||
The above "color-of-the-shape" function is not injective, since two distinct shapes (the red triangle and the red rectangle) are assigned the same value. Moreover, it is not surjective, since the image of the function contains only three, but not all five colors in the codomain. |
|||
==General properties== |
|||
In this section, we describe general properties of functions, that are independent of specific properties of the domain and the codomain. |
|||
===Canonical functions=== |
|||
Some functions are uniquely defined by their domain and codomain, and are sometimes called ''canonical'': {{anchor|Empty function}} |
|||
* For every set {{mvar|X}}, there is a unique function, called the '''empty function''' from the [[empty set]] to {{mvar|X}}. This function is not interesting by itself, but useful for simplifying statements, similarly as the [[empty sum]] (equal to 0) and the [[empty product]] equal to 1. |
|||
* For every set {{mvar|X}} and every [[singleton set]] {{math|{''s''}{{void}}}}, there is a unique function, called the '''canonical surjection''', from {{mvar|X}} to {{math|{''s''}{{void}}}}, which maps to {{mvar|s}} every element of {{mvar|X}}. This is a surjection (see below), except if {{mvar|X}} is the empty set. |
|||
* Given a function <math>f\colon X\to Y,</math> the '''canonical surjection''' of {{mvar|f}} onto its ''image'' <math>f(X)=\{f(x)\mid x\in X\}</math> is the function from {{mvar|X}} to {{math|''f''(''X'')}} that maps {{mvar|x}} to {{math|''f''(''x'')}} |
|||
* For every [[subset]] {{mvar|X}} of a set {{mvar|Y}}, the '''[[canonical injection]]''' of {{mvar|X}} into {{mvar|Y}} is the injective (see below) function that maps every element of {{mvar|X}} to itself. |
|||
* The [[identity function]] of {{mvar|X}}, often denoted by <math>\operatorname{id}_X</math> is the canonical injection of {{mvar|X}} into itself. |
|||
===Function composition=== |
===Function composition=== |
||
{{Main|Function composition}} |
{{Main|Function composition}} |
||
The ''function composition'' of two functions takes the output of one function as the input of a second one. More specifically, the composition of ''f'': ''X'' → ''Y'' with a function ''g'': ''Y'' → ''Z'' is the function <math>g \circ f\colon X \rightarrow Z</math> defined by |
|||
Given two functions <math>f:X\to Y</math> and <math>g:Y\to Z</math> such that the domain of {{mvar|g}} is the codomain of {{mvar|f}}, their ''composition'' is the function <math>g \circ f\colon X \rightarrow Z</math> defined by |
|||
:<math>(g \circ f)(x) = g(f(x)).</math> |
:<math>(g \circ f)(x) = g(f(x)).</math> |
||
That is, the value of ''x'' is obtained by first applying ''f'' to ''x'' to obtain ''y'' = ''f''(''x'') and then applying ''g'' to ''y'' to obtain ''z'' = ''g''(''y''). In the notation <math>g\circ f</math>, the function on the right, ''f'', acts first and the function on the left, ''g'' acts second, reversing English reading order. The notation can be memorized by reading the notation as "''g'' of ''f''" or "''g'' after ''f''". |
|||
That is, the value of <math>g \circ f</math> is obtained by first applying {{math|''f''}} to {{math|''x''}} to obtain {{math|1=''y'' =''f''(''x'')}} and then applying {{math|''g''}} to the result {{mvar|y}} to obtain {{math|1=''g''(''y'') = ''g''(''f''(''x''))}}. In the notation the function that is applied first is always written on the right. |
|||
The composition <math>g\circ f</math> is only defined when the codomain of ''f'': ''X'' → ''Y'' is the domain of ''g'': ''Y'' → ''Z''. |
|||
For that reason composition is not commutative, only when both functions are closed on the same domain, i.e. the domain and the codomain are the same <math>f,g:X\to X</math>, they can be composed in both ways <math>f\circ g</math> and <math>g\circ f</math>. But it '''does not imply''' that <math>f\circ g</math> and <math>g\circ f</math> are the same function. |
|||
The composition <math>g\circ f</math> is an [[operation (mathematics)|operation]] on functions that is defined only if the codomain of the first function is the domain of the second one. Even when <math>g \circ f</math> and <math>f \circ g</math> are both defined, the composition is not [[commutative property|commutative]]. For example, if {{math|1=''f''(''x'') = ''x''<sup>2</sup>}} and {{math|1=''g''(''x'') = ''x'' + 1}}, one has <math>g(f(x))=x^2+1\neq f(g(x)) = (x+1)^2.</math> |
|||
The function composition is [[associative property|associative]] in the sense that, if one of <math>(h\circ g)\circ f</math> and <math>h\circ (g\circ f)</math> is defined, then the other is also defined, and they are equal. Thus, one writes |
|||
:<math>h\circ g\circ f = (h\circ g)\circ f = h\circ (g\circ f).</math> |
|||
The [[identity function]]s <math>\operatorname{id}_X</math> and <math>\operatorname{id}_Y</math> are respectively a [[right identity]] and a [[left identity]] for functions from {{mvar|X}} to {{mvar|Y}}. That is, if {{mvar|f}} is a function with domain {{mvar|X}}, and codomain {{mvar|Y}}, one has |
|||
<math>f\circ \operatorname{id}_X = \operatorname{id}_Y \circ f = f.</math> |
|||
<gallery widths="250" heights="300"> |
<gallery widths="250" heights="300"> |
||
File:Function machine5.svg|A composite function ''g''(''f''(''x'')) can be visualized as the combination of two "machines". |
File:Function machine5.svg|A composite function ''g''(''f''(''x'')) can be visualized as the combination of two "machines". |
||
File:Example for a composition of two functions.svg|A |
File:Example for a composition of two functions.svg|A simple example of a function composition |
||
File:Compfun.svg|Another composition. For example, we have here {{math|1=(''g'' ∘ ''f'' )(c) = #}}. |
File:Compfun.svg|Another composition. For example, we have here {{math|1=(''g'' ∘ ''f'' )(c) = #}}. |
||
</gallery> |
</gallery> |
||
=== |
===Image and preimage=== |
||
{{Main| |
{{Main|Image (mathematics)}} |
||
Let <math>f\colon X\to Y.</math> The ''image'' by {{mvar|f}} of an element {{mvar|x}} of the domain {{mvar|X}} is {{math|''f''(''x'')}}. If {{math|''A''}} is any subset of {{math|''X''}}, then the ''image'' of {{mvar|A}} by {{mvar|f}}, denoted {{math|''f''(''A'')}} is the subset of the codomain {{math|''Y''}} consisting of all images of elements of {{mvar|A}}, that is, |
|||
The unique function over a set ''X'' that maps each element to itself is called the ''identity function'' for ''X'', and typically denoted by id<sub>''X''</sub>. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ''f'' is any function from ''X'' to ''Y'', then |
|||
:<math>\ |
:<math>f(A)=\{f(x)\mid x\in A\}.</math> |
||
f \circ \operatorname{id}_X &= f , \\ |
|||
\operatorname{id}_Y \circ f &= f . |
|||
\end{align}</math> |
|||
The ''image'' of {{math|''f''}} is the image of the whole domain, that is {{math|''f''(''X'')}}. It is also called the [[range (mathematics)|range]] of {{mvar|f}}, although the term may also refer to the codomain.<ref name = "standard">''Quantities and Units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology'', page 15. ISO 80000-2 (ISO/IEC 2009-12-01)</ref> |
|||
===Restrictions and extensions===<!-- This section is linked from [[Subgroup]], [[Restriction]], [[Quadratic form]] --> |
|||
{{main|Restriction (mathematics)}} |
|||
Informally, a ''restriction'' of a function ''f'' is the result of trimming its domain. More precisely, if ''S'' is any subset of ''X'', the restriction of ''f'' to ''S'' is the function ''f''|<sub>''S''</sub> from ''S'' to ''Y'' such that ''f''|<sub>''S''</sub>(''s'') = ''f''(''s'') [[Universal quantification|for all]] ''s'' in ''S''. If ''g'' is a restriction of ''f'', then it is said that ''f'' is an ''extension'' of ''g''. |
|||
On the other hand, the ''[[inverse image]]'', or ''[[preimage]]'' by {{mvar|f}} of a subset {{math|''B''}} of the codomain {{math|''Y''}} is the subset of the domain {{math|''X''}} consisting of all elements of {{math|''X''}} whose images belong to {{math|''B''}}. It is denoted by <math>f^{-1}(B).</math> That is |
|||
The ''overriding'' of ''f'': ''X'' → ''Y'' by ''g'': ''W'' → ''Y'' (also called ''overriding union'') is an extension of ''g'' denoted as (''f'' ⊕ ''g''): (''X'' ∪ ''W'') → Y. Its graph is the set-theoretical union of the graphs of ''g'' and ''f''|<sub>''X'' \ ''W''</sub>. Thus, it relates any element of the domain of ''g'' to its image under ''g'', and any other element of the domain of ''f'' to its image under ''f''. Overriding is an [[associative operation]]; it has the empty function as an [[identity element]]. If ''f''|<sub>''X'' ∩ ''W''</sub> and ''g''|<sub>''X'' ∩ ''W''</sub> are pointwise equal (e.g., the domains of ''f'' and ''g'' are disjoint), then the union of ''f'' and ''g'' is defined and is equal to their overriding union. This definition agrees with the definition of union for [[binary relation]]s. |
|||
:<math>f^{-1}(B) = \{x \in X \mid f(x) \in B\}.</math> |
|||
For example, the preimage of {4, 9} under the [[square function]] is the set {−3,−2,2,3}. |
|||
By definition of a function, the image of an element {{math|''x''}} of the domain is always a single element of the codomain. However, the preimage of a single element {{mvar|y}}, denoted <math>f^{-1}(x),</math> may be [[empty set|empty]] or contain any number of elements. For example, if {{mvar|f}} is the function from the integers to themselves that map every integer to 0, then {{math|1=''f''<sup>−1</sup>(0) = '''Z'''}}. |
|||
===Inverse function=== |
|||
{{Main|Inverse function}} |
|||
If <math>f\colon X\to Y</math> is a function, {{math|A}} and {{math|B}} are subsets of {{math|X}}, and {{math|C}} and {{math|D}} are subsets of {{math|Y}}, then one has the following properties: |
|||
An ''inverse function'' for ''f'', denoted by ''f''<sup>−1</sup>, is a function in the opposite direction, from ''Y'' to ''X'', satisfying |
|||
* <math>A\subseteq B \Longrightarrow f(A)\subseteq f(B)</math> |
|||
* <math>C\subseteq D \Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)</math> |
|||
That is, the two possible compositions of ''f'' and ''f''<sup>−1</sup> need to be the respective identity maps of ''X'' and ''Y''. |
|||
* <math>A \subseteq f^{-1}(f(A))</math> |
|||
* <math>C \supseteq f(f^{-1}(C))</math> |
|||
* <math>f(f^{-1}(f(A)))=f(A)</math> |
|||
* <math>f^{-1}(f(f^{-1}(C)))=f^{-1}(C)</math> |
|||
The preimage by {{mvar|f}} of an element {{mvar|y}} of the codomain is sometimes called, in some contexts, the [[fiber (mathematics)|fiber]] of {{math|''y''}} under {{mvar|''f''}}. |
|||
As a simple example, if ''f'' converts a temperature in degrees Celsius ''C'' to degrees Fahrenheit ''F'', the function converting degrees Fahrenheit to degrees Celsius would be a suitable ''f''<sup>−1</sup>. |
|||
:<math>\begin{align} |
|||
f(C) &= \frac {9}{5} C + 32 \\ |
|||
f^{-1}(F) &= \frac {5}{9} (F - 32) |
|||
\end{align}</math> |
|||
If a function {{mvar|f}} has an inverse (see below), this inverse is denoted <math>f^{-1}.</math> In this case <math>f^{-1}(C)</math> may denote either the image by <math>f^{-1}</math> or the preimage by {{mvar|f}} of {{mvar|C}}. This is not a problem, as these sets are equal. The notation <math>f(A)</math> and <math>f^{-1}(C)</math> may be ambiguous in the case of sets that contain some subsets as elements, such as <math>\{x, \{x\}\}.</math> In this case, some care may be needed, for example, by using square brackets <math>f[A], f^{-1}[C]</math> for images and preimages of subsets, and ordinary parentheses for images and preimages of elements. |
|||
Such an inverse function exists if and only if ''f'' is bijective. In this case, ''f'' is called invertible. The notation <math>g \circ f</math> (or, in some texts, just <math>gf</math>) and ''f''<sup>−1</sup> are akin to multiplication and reciprocal notation. With this analogy, identity functions are like the [[multiplicative identity]], 1, and inverse functions are like [[Multiplicative inverse|reciprocals]] (hence the notation). |
|||
===Injective, surjective and bijective functions=== |
|||
===Empty function=== |
|||
For any set ''A'', there is exactly one function from the empty set to ''A'', namely the ''empty function'': |
|||
Let <math>f\colon X\to Y</math> be a function. |
|||
The function {{mvar|f}} is ''[[injective function|injective]]'' (or ''one-to-one'', or is an ''injection'') if {{math|''f''(''a'') ≠ ''f''(''b'')}} for any two different elements {{math|''a''}} and {{mvar|''b''}} of {{mvar|X}}. Equivalently, {{mvar|f}} is injective if, for any <math>y\in Y,</math> the preimage <math>f^{-1}(y)</math> contains at most one element. An empty function is always injective. If {{mvar|X}} is not the empty set, and if, as usual, the [[axiom of choice]] is assumed, then {{mvar|f}} is injective if and only if there exists a function <math>g\colon y\to X</math> such that <math>g\circ f=\operatorname{id}_X,</math> that is, if {{mvar|f}} has a [[left inverse function|left inverse]]. The axiom of choice is needed, because, if {{mvar|f}} is injective, one defines {{mvar|g}} by <math>g(y)=x</math> if <math>y=f(x),</math> and by <math>g(y)=x_0</math>, if <math>y\not\in f(X),</math> where <math>x_0</math> is an ''arbitrarily chosen'' element of {{mvar|X}}. |
|||
The [[graph of a function|graph]] of an empty function is a [[subset]] of the [[Cartesian product]] {{math|∅ × ''A''}}. Since the product is empty the only such subset is the empty set {{math|∅}}. The empty subset is a valid graph since for every {{math|''x''}} in the domain {{math|∅}} there is a unique {{math|''y''}} in the [[codomain]] {{math|''A''}} such that {{math|(''x'', ''y'') ∈ ∅ × ''A''}}. This statement is an example of a [[vacuous truth]] since "there is no {{math|''x''}} in the domain." |
|||
The function {{mvar|f}} is ''[[surjective]]'' (or ''onto'', or is a ''surjection'') if the range is equals the codomain, that is, if {{math|1=''f''(''X'') = ''Y''}}. In other words, the preimage <math>f^{-1}(y)</math> of every <math>y\in Y</math> is nonempty. If, as usual, the axiom of choice is assumed, then {{mvar|f}} is surjective if and only if there exists a function <math>g\colon y\to X</math> such that <math>f\circ g=\operatorname{id}_Y,</math> that is, if {{mvar|f}} has a [[left inverse function|right inverse]]. The axiom of choice is needed, because, if {{mvar|f}} is injective, one defines {{mvar|g}} by <math>g(y)=x,</math> where <math>x</math> is an ''arbitrarily chosen'' element of <math>f^{-1}(y).</math> |
|||
In [[category theory]] the existence of an empty function from {{math|∅}} to {{math|∅}} is required to make the [[category of sets]] a category, because in a category each object needs to have an "[[identity morphism]]", and only the empty function is the identity on the object {{math|∅}}. |
|||
The existence of a unique empty function from {{math|∅}} into each set {{math|''A''}} means that the empty set is an [[initial object]] in the category of sets. In terms of [[cardinal arithmetic]], it means that {{math|''k''<sup>0</sup> {{=}} 1}} for every [[cardinal number]] {{math|''k''}}—particularly profound when [[0^0|{{math|''k'' {{=}} 0}}]] to illustrate the strong statement of indices pertaining to {{math|0}}. |
|||
The function {{mvar|f}} is ''[[bijective]]'' (or is ''bijection'' or a ''one-to-one correspondence'') if it is both injective and surjective. That is {{mvar|f}} is bijective if, for any <math>y\in Y,</math> the preimage <math>f^{-1}(y)</math> contains exactly one element. The function {{mvar|f}} is bijective if and only if it admits an [[inverse function]], that is a function <math>g\colon y\to X</math> such that <math>g\circ f=\operatorname{id}_X,</math> and <math>f\circ g=\operatorname{id}_Y.</math> (Contrarily to the case of injections and surjections, this does not require the axiom of choice.) |
|||
==Types of functions== |
|||
{{For|a more extensive list|list of types of functions}} |
|||
Every function <math>f\colon X\to Y</math> may be [[factorization|factorized]] as the composition {{math|''i'' ∘ ''s''}} of a surjection followed by an injection, where {{mvar|s}} is the canonical surjection of {{mvar|X}} onto {{math|''f''(''X'')}}, and {{mvar|i}} is the canonical injection of {{math|''f''(''X'')}} into {{mvar|Y}}. This is the ''canonical factorization'' of {{mvar|f}}. |
|||
===Real-valued functions=== |
|||
A [[real-valued function]] ''f'' is one whose codomain is the set of [[real numbers]] or a [[subset]] thereof. If, in addition, the domain is also a subset of the reals, ''f'' is a real valued function of a real variable. The study of such functions is called [[real analysis]]. |
|||
"One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the [[Nicolas Bourbaki|Bourbaki group]] and imported into English. As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "{{math|''f''}} maps {{math|''X''}} ''onto'' {{math|''Y''}}" differs from "{{math|''f''}} maps {{math|''X''}} ''into'' {{math|''B''}}" in that the former implies that {{math|''f''}} is surjective), while the latter makes no assertion about the nature of {{math|''f''}} the mapping. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage to be more symmetrical. |
|||
Real-valued functions enjoy so-called pointwise operations. That is, given two functions |
|||
:<math>f,g : X \to \mathbb{R},</math> |
|||
where ''X'' is an arbitrary set, their (pointwise) sum {{nowrap|''f'' + ''g''}} and product {{nowrap|''f'' ⋅ ''g''}} are functions with the same domain and codomain. They are defined by the formulas: |
|||
:<math>\begin{align} |
|||
(f + g)(x) &= f(x) + g(x), \\ |
|||
(f \cdot g)(x) &= f(x) \cdot g(x). |
|||
\end{align}</math> |
|||
===Restriction and extension{{anchor|Restrictions and extensions}}===<!-- This section is linked from [[Subgroup]], [[Restriction]], [[Quadratic form]] --> |
|||
In a similar vein, [[complex analysis]] studies functions whose domain and codomain are both the set of [[complex numbers]]. In most situations, the domain and codomain are understood from context, and only the relationship between the input and output is given, but if <math>f(x) = \sqrt{x}</math>, then in real variables the domain is limited to non-negative numbers. |
|||
{{main|Restriction (mathematics)}} |
|||
If <math>f\colon X\to Y</math> is a function, and {{mvar|S}} is a subset of {{mvar|X}}, then the ''restriction'' of {{mvar|f}} to {{mvar|S}}, denoted {{math|''f''<sub>{{!}}''S''</sub>}}, is the function from {{mvar|S}} to {{mvar|Y}} that is defined by |
|||
:<math>f_{|S}(x)= f(x)\quad \text{for all } x\in S.</math> |
|||
This often used for define partial inverse functions: if there is a subset {{mvar|S}} of a function {{mvar|f}} such that {{math|''f''<sub>{{!}}''S''</sub>}} is injective, then the canonical surjection of {{math|''f''<sub>{{!}}''S''</sub>}} on its image {{math|1=''f''<sub>{{!}}''S''</sub>(''S'') = ''f''(''S'')}} is a bijection, which has an inverse function from {{math|''f''(''S'')}} to {{mvar|S}}. This is in this way that [[inverse trigonometric functions]] are defined. The [[cosine function]], for example, is injective, when restricted to the [[interval (mathematics)|interval]] {{math|(–0, {{pi}})}}; the image of this restriction is the interval {{math|(–1, 1)}}; this defines thus an inverse function from {{math|(–1, 1)}} to {{math|(–0, {{pi}})}}, which is called [[arccosine]] and denoted {{math|arccos}}. |
|||
The following table contains a few particularly important types of real-valued functions: |
|||
{| class="wikitable" style="text-align: center;" |
|||
|- |
|||
! style="width: 50%;"| [[Linear function]] !! style="width: 50%;"| [[Quadratic function]] |
|||
|- |
|||
| [[File:Gerade.svg|thumb|A linear function|center]] || [[File:Polynomialdeg2.svg|thumb|A quadratic function.|center]] |
|||
|- |
|||
| <math>f(x) = ax + b</math> || <math>f(x) = ax^2 + bx + c</math> |
|||
|- |
|||
! [[Discontinuous function]] !! [[Trigonometric functions]] |
|||
|- |
|||
| [[File:Signum function.svg|thumb|The [[signum function]] is not continuous, since it "jumps" at 0.|center]] || |
|||
[[File:Sine cosine one period.svg|thumb|The sine and cosine functions.|center]] |
|||
|- |
|||
| Roughly speaking, a continuous function is one whose graph can be drawn without lifting the pen. || <math>f(x) = \sin x</math> (red), <math>f(x) = \cos x</math> (blue) |
|||
|} |
|||
Function restriction may also be used for "gluing" functions together: let <math>\textstyle X=\bigcup_{i\in I}U_i</math> be the decomposition of {{mvar|X}} as a [[set union|union]] of subsets. Suppose that a function <math>f_i\colon U_i\to Y</math> is defined on each <math>U_i,</math> such that, for each pair of indices, the restrictions of <math>f_i</math> and <math>f_j</math> to <math>U_i\cap U_j</math> are equal. Then, this defines a unique function <math>f\colon X\to Y</math> such that <math>f_{|U_i} =f_i</math> for every {{mvar|i}}. This is generally in this way that functions on [[manifold]]s are defined. |
|||
==={{vanchor|Multivariate function|MULTIVARIATE_FUNCTION}}s=== |
|||
An ''extension'' of a function {{mvar|f}} is a function {{mvar|g}} such that {{mvar|f}} is a restriction of {{mvar|g}}. A typical use of this concept is the process of [[analytic continuation]], that allows extending functions whose domain is a small part of the [[complex plane]] to functions whose domain is almost the whole complex plane. |
|||
A [[multivariate function]] is one which takes several inputs. |
|||
Here is another classical example of a function extension that is encountered when studying [[homography|homographies]] of the [[real line]]. An ''homography'' is a function <math>h(x)=\frac{ax+b}{cx+d}</math> such that {{math|''ad'' – ''bc'' ≠ 0}}. Its domain is the set of all [[real number]]s different from <math>-d/c,</math> and its image is the set of all real numbers different from <math>a/b.</math> If one extends the real line to the [[projectively extended real line]] by adding {{math|∞}} to the real numbers, one may extend {{mvar|h}} for being a bijection of the extended real line to itself, by setting <math>h(\infty)=a/b</math> and <math>h(-d/c)=\infty.</math> |
|||
===Further types of functions=== |
|||
{{Further|List of mathematical functions}} |
|||
There are many other special classes of functions that are important to particular branches of mathematics, or particular applications. |
|||
Here is a partial list: |
|||
{{div col|colwidth=20em}} |
|||
*[[differentiable function|differentiable]], [[integrable function|integrable]] |
|||
*[[polynomial]], [[rational function|rational]] |
|||
*[[algebraic function|algebraic]], [[transcendental function|transcendental]] |
|||
*[[even and odd functions|odd or even]] |
|||
*[[convex function|convex]], [[monotonic function|monotonic]] |
|||
*[[holomorphic function|holomorphic]], [[Meromorphic function|meromorphic]], [[Entire function|entire]] |
|||
*[[vector-valued function|vector-valued]] |
|||
*[[computable function|computable]] |
|||
{{div col end}} |
|||
==Multivariate function {{anchor|MULTIVARIATE_FUNCTION}}== |
|||
==Function spaces== |
|||
[[File:Binary operations as black box.svg|thumb|A binary operation is a typical example of a bivariate, function which assigns to each pair <math>(x, y)</math> the result <math>x\circ y</math>.]] |
|||
{{Main|Function space}} |
|||
A '''multivariate function''', or '''function of several variables''' is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time and its speed. |
|||
The set of all functions from a set ''X'' to a set ''Y'' is denoted by ''X'' → ''Y'', by [''X'' → ''Y''], or by ''Y''<sup>''X''</sup>. The latter notation is motivated by the fact that, when ''X'' and ''Y'' are finite and of [[Cardinality|size]] |''X''| and |''Y''|, then the number of functions ''X'' → ''Y'' is |''Y''<sup>''X''</sup>| = |''Y''|<sup>|''X''|</sup>. This is an example of the convention from enumerative combinatorics that provides notations for sets based on their cardinalities. If ''X'' is [[infinity|infinite]] and there is more than one element in ''Y'' then there are [[uncountable set|uncountably many]] functions from ''X'' to ''Y'', though only countably many of them can be expressed with a formula or algorithm. |
|||
More formally, a function of {{mvar|n}} variables is a function whose domain is a set of [[tuple|{{mvar|n}}-tuples]]. |
|||
===Currying=== |
|||
For example, multiplication of [[integer]]s is a function of two variables, or '''bivariate function''', whose domain it the set of all pairs (2-uples) of integers and the codomain is the set of integers. The same is true for every [[binary operation]]. More generally, every [[mathematical operation]] is defined as a multivariate function. |
|||
{{Main|Currying}} |
|||
The [[direct product]] <math>X_1\times\cdots\times X_n</math> of {{mvar|n}} sets <math>X_1, \ldots, X_n</math> is the set of all {{mvar|n}}-uples <math>(x_1, \ldots, x_n)</math> such that <math>x_i\in X_i</math> for every {{mvar|i}}. Therefore, a function of {{mvar|n}} variables is a function |
|||
An alternative approach to handling functions with multiple arguments is to transform them into a chain of functions that each takes a single argument. For instance, one can interpret Add(3,5) to mean "first produce a function that adds 3 to its argument, and then apply the 'Add 3' function to 5". This transformation is called [[currying]]: Add 3 is curry(Add) applied to 3. There is a [[bijection]] between the function spaces ''C''<sup>''A''×''B''</sup> and (''C''<sup>''B''</sup>)<sup>''A''</sup>. |
|||
:<math>f:U\to Y,</math> |
|||
where the domain {{mvar|U}} has the form |
|||
:<math>U\subseteq X_1\times\cdots\times X_n.</math> |
|||
When using the functional notation, one omits the parentheses surrounding tuples. That is, one write <math>f(x_1,x_2)</math>, and not <math>f((x_1,x_2)).</math> |
|||
In the case where all <math>X_i</math>s are equal to the set <math>\R</math> of [[real number]]s, one has a [[function of several real variables]]. If the <math>X_i</math>s are equal to the set <math>\C</math> of [[complex number]]s, one has a [[function of several complex variables]] |
|||
When working with curried functions it is customary to use prefix notation with function application considered left-associative, since juxtaposition of multiple arguments—as in (''f'' ''x'' ''y'')—naturally maps to evaluation of a curried function. Conversely, the → and ⟼ symbols are considered to be right-associative, so that curried functions may be defined by a notation such as ''f'': ℤ → ℤ → ℤ = ''x'' ⟼ ''y'' ⟼ ''x''·''y''. |
|||
It is common to consider also functions whose codomain is a product of sets. For example, [[Euclidean division]] maps very pair {{math|(''a'', ''b'')}} of integers with {{math|''b'' ≠ 0}} to a pair of integers called the ''quotient'' and the ''remainder''. |
|||
==Variants and generalizations== |
|||
:<math>\begin{align} |
|||
\text{Euclidean division}\colon &\quad\Z\times (\Z\setminus \{0\}) \to \Z\times\Z\\ |
|||
&(a,b)\to (\operatorname{quotient}(a,b),\operatorname{remainder}(a,b)). |
|||
\end{align}</math> |
|||
The codomain may also be a [[vector space]]. In this case, one talks of a [[vector-valued function]]. If the domain is contained in a [[Euclidean space]], or more generally a [[manifold]], a vector-valued function is often called a [[vector field]]. |
|||
==In calculus== |
|||
===Definitions used in set theory=== |
|||
The definitions of '''function''' and '''image''' in [[set theory]] are more general than the ones given above—namely, the definition of function does not mention a domain or a codomain, and the definition of the image ''F''[''A''] does not require that ''A'' be a subset of the domain.<ref>This definition of image is used in the proof that NBG's axiom of replacement implies NBG's axiom of separation. See [[NBG's axiom of separation]].</ref> Set theory also specializes its function definition to the cases where the domain or both the domain and codomain are specified. This produces the following three definitions.<ref>{{harvnb |Gödel |1940 |p=16}}; {{harvnb |Jech |2003 |p=11}}; {{harvnb |Cunningham |2016 |p=57}}. Gödel gives definitions 1 and 2 (he uses "over ''X''{{space|hair}}" instead of "on ''X''{{space|hair}}" in definition 2). Jech gives all three definitions; Cunningham gives definitions 1 and 3.</ref> |
|||
#{{space|hair}}''F'' is a {{em|function}} if ''F'' is a set or [[Class (set theory)|class]] of ordered pairs such that for all ''x, y,'' and ''z:'' If (''x'', ''y'') ∈ F and (''x'', ''z'') ∈ F, then ''y'' = ''z''. |
|||
#{{space|hair}}''F'' is a {{em|function on X}}{{space|hair}} if ''F'' is a function and ''X'' is the domain of ''F''. |
|||
#{{space|hair}}''F'' is a {{em|function from X to Y}}{{space|hair}} if ''F'' is a function, ''X'' is the domain of ''F'', and ''F''[''X''] ⊆ ''Y''. |
|||
The idea of function, starting in the 17th century, was fundamental to the new [[infinitesimal calculus]] (see [[History of the function concept]]). At that time, only [[real-valued function|real-valued]] functions of a [[function of a real variable|real variable]] were considered, and all functions were assumed to be [[smooth function|smooth]]. But the definition was soon extended to [[#Multivariate function|functions of several variables]] and to [[function of a complex variable]]. In the second half of 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined. |
|||
The first definition allows the use of functions without specifying their domain or codomain. For example, this definition is used to state the [[Von Neumann–Bernays–Gödel set theory#NBG's axiom of replacement|replacement axiom of von Neumann–Bernays–Gödel set theory]]: For all classes ''F'' and for all sets ''X'', if ''F'' is a function, then ''F''[''X''] is a set. Since this definition uses set theory's definition of image, ''X'' does not have to be a subset or subclass of the domain of ''F''. |
|||
Functions are now used throughout all areas of mathematics. In introductory [[calculus]], when the word ''function'' is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as [[real analysis]] and [[complex analysis]]. |
|||
The second definition can be used to define a set or class of functions without specifying a codomain. For example, the class of functions on the [[von Neumann ordinal|ordinal]] α. Also, an infinite [[sequence]] can be defined as a function on ω, the set of finite ordinals. |
|||
===Real function=== |
|||
The third definition requires that the function's domain and codomain be specified. For example, the [[aleph function]] <math>\aleph</math> is a function from the class of [[Ordinal number|ordinal]]s to the class of infinite [[cardinal number|cardinal]]s. Its function values are denoted by using a subscript: <math>\aleph_\alpha</math>, rather than by using parentheses: <math>\aleph(\alpha)</math>. The notation <math>\aleph_\alpha</math> extends the [[sequence]] notation <math>x_n</math> into the [[Transfinite number|transfinite]]. |
|||
{{see also|Real analysis}} |
|||
[[File:Gerade.svg|thumb|right|Graph of a linear function]] |
|||
[[File:Polynomialdeg2.svg|thumb|right|Graph of a polynomial function, here a quadratic function.|right]] |
|||
[[File:Sine cosine one period.svg|thumb|right|Graph of two trigonometric functions: [[sine]] and [[cosine]].]] |
|||
A ''real function'' is a [[real-valued function|real-valued]] function of a [[function of a real variable|real variable]], that is, a function whose codomain is the [[real number|field of real numbers]] and whose domain is a set of [[real number]]s that contains an [[interval (mathematics)|interval]]. In this section, these functions are simply called ''functions''. |
|||
The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are [[continuous function|continuous]], [[differentiable function|differentiable]], and even [[analytic function|analytic]]. This regularity insures that these functions can be visualized by their [[#graph|graphs]]. In this section, all functions are differentiable in some interval. |
|||
===Alternative definition of a function=== |
|||
The above definition of "a function from ''X'' to ''Y''" is generally agreed on,{{Citation needed|reason= "generally agreed" unsubstantiated, sampling current literature indicates codomain not in the definition|date=August 2012}} however there are two different ways a "function" is normally defined where the domain ''X'' and codomain ''Y'' are not explicitly or implicitly specified. Usually this is not a problem as the domain and codomain normally will be known. With one definition saying the function defined by {{nowrap|1=''f''(''x'') = ''x''<sup>2</sup>}} on the reals does not completely specify a function as the codomain is not specified, and in the other it is a valid definition. |
|||
Functions enjoy [[pointwise operation]]s, that is, if {{mvar|f}} and {{mvar|g}} are functions, their sum, difference and product are functions defined by |
|||
In the other definition a function is defined as a set of ordered pairs where each first element only occurs once. The domain is the set of all the first elements of a pair and there is no explicit codomain separate from the image.<ref>{{cite book |title=Calculus vol 1 |first=Tom |last=Apostol |authorlink=Tom M. Apostol |page=53 |publisher=John Wiley |isbn=0-471-00005-1 |year=1967}}</ref><ref>{{cite book |last=Heins |first=Maurice |title=Complex function theory |publisher=Academic Press |year=1968 |page=4 |url=https://books.google.com/books?id=OtyBXTOTwZoC&pg=PA4}}</ref> Concepts like [[surjective]] have to be refined for such functions, more specifically by saying that a (given) function is ''surjective on a (given) set'' if its image equals that set. For example, we might say a function ''f'' is surjective on the set of real numbers. |
|||
:<math>\begin{align} |
|||
(f+g)(x)&=f(x)+g(x)\\ |
|||
(f-g)(x)&=f(x)-g(x)\\ |
|||
(f\cdot g)(x)&=f(x)\cdot g(x)\\ |
|||
\end{align}.</math> |
|||
The domains of the resulting functions are the [[set intersection|intersection]] of the domains of {{mvar|f}} and {{mvar|g}}. The quotient of two functions is defined similarly by |
|||
:<math>\frac fg(x)=\frac{f(x)}{g(x)},</math> |
|||
but the domain of the resulting function is obtained by removing the [[zero of a function|zeros]] of {{mvar|g}} from the intersection of the domains of {{mvar|f}} and {{mvar|g}}. |
|||
The [[polynomial function]]s are defined by [[polynomial]]s, and their domain is the whole set of real numbers. They include [[constant function]]s, [[linear function]]s and [[quadratic function]]s. [[Rational function]]s are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid [[division by zero]]. The simplest rational function is the function <math>x\mapsto \frac 1x,</math> whose graph is an [[hyperbola]], and whose domain is the whole [[real line]] except for 0. |
|||
If a function is defined as a set of ordered pairs with no specific codomain, then {{nowrap|''f'': ''X'' → ''Y''}} indicates that ''f'' is a function whose domain is ''X'' and whose image is a subset of ''Y''. This is the case in the ISO standard.<ref name="standard" /> ''Y'' may be referred to as the codomain but then any set including the image of ''f'' is a valid codomain of ''f''. This is also referred to by saying that "''f'' maps ''X'' into ''Y''"<ref name = "standard">''Quantities and Units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology'', page 15. ISO 80000-2 (ISO/IEC 2009-12-01)</ref> In some usages ''X'' and ''Y'' may subset the ordered pairs, e.g. the function ''f'' on the real numbers such that ''y''=''x''<sup>2</sup> when used as in {{nowrap|''f'': [0,4] → [0,4]}} means the function defined only on the interval [0,2].{{sfn |Bartle |1967 |p=13}} With the definition of a function as an ordered triple this would always be considered a [[partial function]]. |
|||
The [[derivative]] of a real differentiable function is a real function. An [[antiderivative]] of a continuous real function is a real function that is differentiable in any [[open interval]] in which the original function is continuous. For example, the function <math>x\mapsto\frac 1x</math> is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for {{math|1=''x'' = 1}}, is a differentiable function called the [[natural logarithm]]. |
|||
An alternative definition of the composite function ''g''(''f''(''x'')) defines it for the set of all ''x'' in the domain of ''f'' such that ''f(x)'' is in the domain of ''g''.{{sfn |Bartle |1967|p=21}} Thus the real square root of −''x''<sup>2</sup> is a function only defined at 0 where it has the value 0. |
|||
A real function {{mvar|f}} is [[monotonic function|monotonic]] in an interval if the sign of <math>\frac{f(x)-f(y)}{x-y}</math> does not depend of the choice of {{mvar|x}} and {{mvar|y}} in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function {{mvar|f}} is monotonic in an interval {{mvar|I}}, it has an [[inverse function]], which is a real function with domain {{math|''f''(''I'')}} and image {{mvar|I}}. This is how [[inverse trigonometric functions]] are defined in terms of [[trigonometric functions]], where the trigonometric functions are monotonic. Another example: the natural logarithm is monotonic on the positive real numbers, and its image is the whole real line; therefore it has an inverse function that is a [[bijection]] between the real numbers and the positive real numbers. This inverse is the [[exponential function]]. |
|||
Functions are commonly defined as a type of [[binary relation|relation]]. A relation from ''X'' to ''Y'' is a set of [[ordered pair]]s {{nowrap|(''x'', ''y'')}} with x ∈ X and y ∈ Y. A function from ''X'' to ''Y'' can be described as a relation from ''X'' to ''Y'' that is left-total and right-unique. However, when ''X'' and ''Y'' are not specified there is a disagreement about the definition of a relation that parallels that for functions. Normally a relation is just defined as a set of ordered pairs and a [[Correspondence (mathematics)|correspondence]] is defined as a triple {{nowrap|(''X'', ''Y'', ''F'')}}, however the distinction between the two is often blurred or a relation is never referred to without specifying the two sets. The definition of a function as a triple defines a function as a type of correspondence, whereas the definition of a function as a set of ordered pairs defines a function as a type of relation. |
|||
Many other real functions are defined either by the [[implicit function theorem]] (the inverse function is a particular instance) or as solutions of [[differential equation]]s. For example the [[sine]] and the [[cosine]] functions are the solutions of the [[linear differential equation]] |
|||
Many operations in set theory, such as the [[power set]], have the [[Class (set theory)|class]] of all sets as their domain, and therefore, although they are informally described as functions, they do not fit the set-theoretical definition outlined above, because a class is not necessarily a set. However some definitions of relations and functions define them as classes of pairs rather than sets of pairs and therefore do include the power set as a function.<ref>{{cite book |title=A formalization of set theory without variables |last1=Tarski |first1=Alfred |authorlink=Alfred Tarski |last2=Givant |first2=Steven |year=1987 |page=3 |publisher=American Mathematical Society |isbn=0-8218-1041-3}}</ref> |
|||
:<math>y''+y=0</math> |
|||
such that |
|||
:<math>\sin 0=0, \quad \cos 0=1, \quad\frac{\partial \sin x}{\partial x}(0)=1, \quad\frac{\partial \cos x}{\partial x}(0)=0.</math> |
|||
===Complex function=== |
|||
===Partial and multi-valued functions=== |
|||
{{main|complex analysis}} |
|||
[[File:Function with two values 1.svg|thumb|right|<math>f(x) = \pm \sqrt x</math> is not a function in the proper sense, but a multi-valued function: it assigns to each positive real number ''x'' two values: the (positive) [[square root]] of ''x'', and <math>-\sqrt x.</math>]] |
|||
{{expand section|date=April 2018}} |
|||
In some parts of mathematics, including [[recursion theory]] and [[functional analysis]], it is convenient to study ''[[partial function]]s'' in which some values of the domain have no association in the graph; i.e., single-valued relations. For example, the function ''f'' such that ''f''(''x'') = 1/''x'' does not define a value for ''x'' = 0, since [[division by zero]] is not defined. Hence ''f'' is only a partial function from the real line to the real line. The term [[total function]] can be used to stress the fact that every element of the domain does appear as the first element of an ordered pair in the graph. |
|||
===Function of several real or complex variables=== |
|||
In other parts of mathematics, non-single-valued relations are similarly conflated with functions: these are called ''[[multivalued function]]s'', with the corresponding term [[single-valued function]] for ordinary functions. |
|||
{{main|Function of several real variables|Function of several complex variables|Scalar field}} |
|||
{{expand section|date=April 2018}} |
|||
===Vector-valued function=== |
|||
===Functions with multiple inputs and outputs=== |
|||
{{main|Vector-valued function|Vector field}} |
|||
The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the [[Cartesian product]] of two or more sets. |
|||
{{expand section|date=April 2018}} |
|||
==Function space== |
|||
For example, consider the function that associates two [[integer]]s to their product: ''f''(''x'', ''y'') = ''x''·''y''. This function can be defined formally as having domain ℤ×ℤ, the set of all integer pairs; codomain ℤ; and, for graph, the set of all pairs ((''x'', ''y''), ''x''·''y''). The first component of any such pair is itself a pair (of integers), while the second component is a single integer. |
|||
{{Main|Function space|Functional analysis}} |
|||
In [[mathematical analysis]], and more specifically in [[functional analysis]], a '''function space''' is a set of [[scalar-valued function|scalar-valued]] or [[vector-valued function]]s, which share a specific property and form a [[topological vector space]]. For example, the real [[smooth function]]s with a [[compact support]] (that is, they are zero outside some [[compact set]]) form a function space that is at the basis of the theory of [[distribution (mathematics)|distributions]]. |
|||
Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and [[topology|topological]] properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of [[ordinary differential equation|ordinary]] or [[partial differential equation]]s result of the study of function spaces. |
|||
The function value of the pair (''x'', ''y'') is ''f''((''x'', ''y'')). However, it is customary to drop one set of parentheses and consider ''f''(''x'', ''y'') a function of two variables, ''x'' and ''y''. Functions of two variables may be plotted on the three-dimensional Cartesian as ordered triples of the form (''x'', ''y'', ''f''(''x'', ''y'')). |
|||
===Multi-valued functions=== |
|||
The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example, consider the integer divide function, with domain ℤ×ℕ and codomain ℤ×ℕ. The resultant (quotient, remainder) pair is a single value in the codomain seen as a Cartesian product. |
|||
{{main|Multi-valued function}} |
|||
[[File:Function with two values 1.svg|thumb|right|Together, the two square roots of all nonnegative real numbers form a single smooth curve.]] |
|||
[[File:Xto3minus3x.svg|thumb|right]] |
|||
Several methods for specifying functions of real or complex variables start from a local definition of the funcion at a point or on a [[neighbourhood (mathematics)|neighbourhood]] of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point <math>x_0,</math> there are several possible starting values for the function. |
|||
For example, for defining the [[square root]] function as the inverse function of the square function, one may choose any positive real number for <math>x_0,</math> and there are two choices for the value of the function, one which is positive and denoted <math>\sqrt {x_0},</math> and the other that is denoted <math>-\sqrt {x_0}.</math> These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one see that, together, they form a single [[smooth curve]]. It is therefore often useful to consider these two square root functions as a single function that has two values for positive {{mvar|x}}, one value for 0 and no value for negative {{mvar|x}}. |
|||
====Binary operations==== |
|||
[[File:Binary operations as black box.svg|thumb|A binary operation is a function which assigns to each pair <math>x</math> and <math>y</math> its result <math>x\circ y</math>.]] |
|||
The familiar [[binary operation]]s of [[arithmetic]], [[addition]] and [[multiplication]], can be viewed as functions from ℝ×ℝ to ℝ. This view is generalized in [[abstract algebra]], where ''n''-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract [[group (mathematics)|group]] is defined as a set ''X'' and a function ''f'' from ''X''×''X'' to ''X'' that satisfies certain properties. |
|||
In the preceding example, one choice, the positive square root, is more natural then the other. This is not the case in general. For example, let consider the [[implicit function]] that maps {{mvar|y}} to a [[root of a function|root]] {{mvar|x}} of <math>x^3-3x-y =0</math> (see the figure on the right). For {{math|1=''y'' = 0}} one may choose either <math>0, \sqrt 3,\text{ or } -\sqrt 3</math> for {{mvar|x.}} By the [[implicit function theorem]], each choice defines a function; for the first one, the (maximal) domain is the interval {{math|[–2, 2]}} and the image is {{math|[–1, 1]}}; for the second one, the domain is {{math|[–2, +∞)}} and the image is {{math|[1, +∞)}}; for the last one, the domain is {{math|(–∞, 2]}} and the image is {{math|(–∞, –1]}}. As the three graphs together form a smooth curve, and there is no reason for preferring one choice, these three functions are often considered as a single ''multi-valued function'' of {{mvar|y}} that has three values for {{math|–2 < ''y'' < 2}}, and only one value for {{math|''y'' ≤ –2}} and {{math|''y'' ≥ –2}}. |
|||
Traditionally, addition and multiplication are written in the [[infix]] notation: ''x''+''y'' and ''x''×''y'' instead of +(''x'', ''y'') and ×(''x'', ''y''). |
|||
Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically [[analytic function]]s. The domain to which a complex function is analytic may be extended by [[analytic continuation]] consists generally of almost the whole [[complex plane]]. However, it is frequent that, when extending the domain through two different paths, one gets different values. For example, when extending the domaine of the square root function, along a path of complex numbers with positive imaginary parts, one gets {{mvar|i}} for the square root of –1, while, when extending through complex numbers with negative imaginary parts, one gets {{math|–''i''}}. There are generally two ways for solving the problem. One may define a function that is not [[continuous function|continuous]] along some curve, called [[branch cut]]. Such a function is called the [[principal value]] of the function. The other way is to consider that one has a ''multi-valued function'', which is analytic everywhere except for isolated singularities, but whose value may "jump" if one follows a closed loop around a singularity. This jump is called the [[monodromy]]. |
|||
===Functors=== |
|||
{{main|Functor}} |
|||
The idea of [[Mathematical structure|structure]]-preserving functions, or [[homomorphism]]s, led to the abstract notion of [[morphism]], the key concept of [[category theory]]. In fact, functions ''f'': ''X'' → ''Y'' are the morphisms in the [[category of sets]], including the empty set: if the domain ''X'' is the [[empty set]], then the subset of ''X'' × ''Y'' describing the function is necessarily empty, too. However, this is still a well-defined function. Such a function is called an [[#Empty function|empty function]]. In particular, the identity function of the empty set is defined, a requirement for sets to form a category. |
|||
==In [[foundations of mathematics]] and [[set theory]]== |
|||
The concept of [[categorification]] is an attempt to replace set-theoretic notions by category-theoretic ones. In particular, according to this idea, sets are replaced by categories, while functions between sets are replaced by [[functor]]s.<ref>{{Cite journal|arxiv=math/9802029|title=Categorification|first=John C.|last=Baez |authorlink=John C. Baez |first2=James|last2=Dolan|year=1998}}</ref> |
|||
The definition of a function that is given in this article requires the concept of [[set (mathematics)|set]], since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is general not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions. |
|||
For example the [[singleton set]] may be considered as a function <math>x\mapsto \{x\}.</math> Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definition for these weakly specified functions.<ref>{{harvnb |Gödel |1940 |p=16}}; {{harvnb |Jech |2003 |p=11}}; {{harvnb |Cunningham |2016 |p=57}}</ref> |
|||
These generalized functions may be critical in the development of a formalization of foundations of mathematics. For example, the [[Von Neumann–Bernays–Gödel set theory]], is an extension of the set theory in which the collection of all sets is a [[Class (set theory)|class]]. This theory includes the [[Von Neumann–Bernays–Gödel set theory#NBG's axiom of replacement|replacement axiom]], which may be interpreted as "if {{mvar|X}} is a set, and {{mvar|F}} is a function, then {{math|''F''[''X'']}} is a set". |
|||
==In computer science== |
|||
{{main|Function (programming)|Lambda calculus}} |
|||
{{expand section|date=April 2018}} |
|||
==See also== |
==See also== |
||
===Subpages=== |
|||
{{div col|3}} |
|||
*[[History of the function concept]] |
|||
*[[List of types of functions]] |
|||
*[[List of functions]] |
|||
*[[Function fitting]] |
|||
*[[Implicit function]] |
|||
{{div col end}} |
|||
===Generalizations=== |
|||
{{div col|3}} |
|||
*[[Homomorphism]] |
|||
*[[Morphism]] |
|||
*[[Distribution (mathematics)|Distribution]] |
|||
*[[Functor]] |
|||
{{div col end}} |
|||
===Related topics=== |
|||
{{div col|3}} |
{{div col|3}} |
||
*[[Associative array]] |
*[[Associative array]] |
||
*[[Functional (mathematics)|Functional]] |
*[[Functional (mathematics)|Functional]] |
||
*[[Functional decomposition]] |
*[[Functional decomposition]] |
||
*[[Function fitting]] |
|||
*[[Functional predicate]] |
*[[Functional predicate]] |
||
*[[Functional programming]] |
*[[Functional programming]] |
||
*[[Generalized function]] |
|||
*[[History of the function concept]] |
|||
*[[Implicit function]] |
|||
*[[List of functions]] |
|||
*[[Parametric equation]] |
*[[Parametric equation]] |
||
{{div col end}} |
|||
{{div col end}} |
{{div col end}} |
||
Revision as of 14:01, 22 April 2018
| Function |
|---|
| x ↦ f (x) |
| History of the function concept |
| Examples of domains and codomains |
| Classes/properties |
| Constructions |
| Generalizations |
In mathematics, a function[1] is originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of the time. Historically, the concept was elaborated with the infinitesimal calculus at the end of 17th century, and, until the 19th century, the function that were considered were differentiable (that is they have a high degree of regularity). The concept of function has been formalized at the end of the 19th century in terms of set theory, and this has much enlarged the domains of application of the concept.
A function is a process or a relation that associates each element x of a set X, the domain of the function, to a unique element y of another set Y (possibly the same set), the codomain of the function. If the function is called f, this relation is denoted y = f (x) (read f of x), the element x is the argument or input of the function, and y is the value of the function, the output, or the image of x by f. The symbol that is used for representing the input is the variable of the function (one says often that f is a function of the variable x).[2]
A function is uniquely represented by its graph which is the set of all pairs (x, f (x)). When the domain and the codomain are sets of numbers, each such pair may be considered as the Cartesian coordinates of a point in the plane. In general, these points form a curve, which is also called the graph of the function. This is a useful representation of the function, which is commonly used everywhere, for example in newspapers.
Functions are widely used in science, and in most fields of mathematics. Their role is so important that it has been said the they are "the central objects of investigation" in most fields of mathematics.[3]

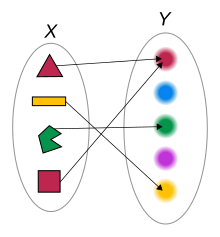
Definition
When students first begin to study functions, intuitive ideas such as "rules" and "associates" are used. In more advanced mathematics, more precise definitions are needed. The precise mathematical definition of a function relies on the notion of an ordered pair.
A function f from X to Y is defined by a set of ordered pairs (x, y) such that x ∈ X and y ∈ Y, which is subject to the following condition: every element of X is the first component of one and only one ordered pair in the set.[4] In other words, for every x in X there is exactly one element y such that the ordered pair (x, y) belongs to the set of pairs defining the function f.
In this definition, X and Y are respectively called the domain and the codomain of the function f. If (x, y) belongs to the set defining f, then y is the value of f for the argument x, or the image of x under f. One says also that y is the value of f for the value x of the variable.
The range denotes generally the image of a function, that is the set of all images of elements of the domain. However it is sometimes used as a synonym of codomain, generally in old textbooks.
Notation
A function f with domain X and codomain Y is commonly denoted
or
The notation
means that (x, y) belongs to the set of pairs defining the function f. When it is needed to refer explicitly to this set of pairs, it is denoted
The symbol used to denote a particular function consists generally of a single letter in italic font, most often the lower-case letters f, g, h. Some widely used functions are represented by a symbol consisting of several letters (generally an abbreviation of their name). In this case, it is set in roman type, such as "sin" for the sine function.
Sometimes the parentheses of the functional notation are omitted if no ambiguity arises, as for instead of
In many cases, a function is defined by a formula that describes how the value of the function is computed from the value of the argument. For example, if a multiplication is defined on a set X, then one may define a square function with domain and codomain X by
or, more commonly,
Similarly, the identity function on a set X is the function
This notation is useful for avoiding naming a function when not necessary, as in the sentence "the square function is the function
The definition of a function by a formula may use case distinction as for the definition of the absolute value of real numbers:
Normally the definition of a function includes the definition of its domain and its codomain, but it is not always the case. Typically, a function from the reals to the reals does not always refer to a function that has the real numbers a domain. This refers often to a function which has a subset of the reals as domain. In many cases some computation is needed if one want to know the domain exactly (see partial function). For example, if f is a function that has the real numbers as domain and codomain, then is a (possibly partial) function from the reals to the reals whose domain is the set of the reals x such that f(x) ≠ 0. In many cases, this set is difficult to determine exactly, and often, this is not a problem for working with the function.
When the domain of a function is the set of natural numbers, one talks often of a sequence (mathematics), and one uses the index notation, that is, one denotes
the image of the nonnegative integer n by the function or sequence f. One says also that is the nth element of the sequence.
Finally, dot notation is occasionally used for avoiding naming the variable. For example, may stand for , and may stand for the integral function .
Specifying a function
In general, a specific function is defined by associating to every element of the domain a property of this element (as in the above example of colored shapes) or the result of a computation taking as input. This computation may be described by a formula. (This is the starting point of algebra of replacing many similar computations on numbers by a single formula that describes the computation on variables representing unspecified numbers). This definition of a function uses frequently previously defined auxiliary functions.
For example, the function f from the reals to the reals, defined by use the square function and the square root function as auxiliary functions. The domain of f is the whole set of real numbers, even if domain of the square root function is restricted to the positive real numbers.
The computation that allows defining a function may often be described by an algorithm, and any kind of algorithm may be used. Sometimes, the definition of a function may involve elements or properties that can be defined, but not computed. For example, if one, consider the set of the programs in a given programming language, which take an integer as input. The terminating function is the function that returns 1 if a progam of runs for ever when executed on a given integer input, and returns 0 otherwise. It is a basic theorem of computability theory that it cannot exist an algorithm for computing this function.
More generally, the computability theory is the study of the computable functions, that is the functions that can be computed by an algorithm.
Above ways of defining functions define them "pointwise", that is, each value is defined independently of the other values. This is not always the case.
When the domain of a function is the nonnegative integers or, more generally, when the domain may be well ordered, a function may be defined by induction or recursion, which means (roughly) that the definition of the function for a given input depends on previously defined values of the function. For example, the Fibonacci sequence is a function from the natural numbers into themselves that is defined by (see above for the use of indices for the argument of a function)
In calculus, the functions that are considered have some regularity. That is, the value of the function at a point is related with the values of the function at neighbor points. This allows defining them by functional equations (the gamma function is the unique meromorphic function such that and ), by differential equations (the natural logarithm is the solution of the differential equation such that ln(1) = 0), integral equations or analytic continuation.
Representing a function
As functions may be complicated objects, it is often useful to draw the graph of a function for getting a global view of its properties. Some functions may also represented histograms
Graph
Given a function its graph is, formally, the set
In the frequent case where X and Y are subsets of the real numbers (or may be identified to such subsets), an element may be identified with the point of coordinates x, y in the Cartesian plane. Marking these points provides a drawing, generally a curve, that is also called the graph of the function. For example the graph of the square function
is a parabola that consists of all points of coordinates for
It is possible to draw effectively the graph of a function only if the function is sufficiently regular, that is, either if the function is differentiable (or piecewise differentiable) or if its domain may be identified with the integers or a subset of the integers.
If either the domain or the codomain of the function is a subset of the graph is a subset of a Cartesian space of higher dimension, and various technics have been developed for drawing it, including the use of colors for representing one of the dimensions.[citation needed]
Histogram
Histograms are often used for representing functions whose domain is finite, or is the natural numbers or the integers. In this case, an element x of the domain is represented by an interval of the x-axis, and a point (x, y) of the graph is represented by a rectangle with basis the interval corresponding to x and height y.
In statistic, histogram are often used for representing very irregular functions. For example, for representing the function that associates his weight to each member of some population, one draws the histogram of the function that associates to each weight interval the number of people, whose weights belong to this interval.
There are many variants of this method, see Histogram for details.
General properties
In this section, we describe general properties of functions, that are independent of specific properties of the domain and the codomain.
Canonical functions
Some functions are uniquely defined by their domain and codomain, and are sometimes called canonical:
- For every set X, there is a unique function, called the empty function from the empty set to X. This function is not interesting by itself, but useful for simplifying statements, similarly as the empty sum (equal to 0) and the empty product equal to 1.
- For every set X and every singleton set {s}, there is a unique function, called the canonical surjection, from X to {s}, which maps to s every element of X. This is a surjection (see below), except if X is the empty set.
- Given a function the canonical surjection of f onto its image is the function from X to f(X) that maps x to f(x)
- For every subset X of a set Y, the canonical injection of X into Y is the injective (see below) function that maps every element of X to itself.
- The identity function of X, often denoted by is the canonical injection of X into itself.
Function composition
Given two functions and such that the domain of g is the codomain of f, their composition is the function defined by
That is, the value of is obtained by first applying f to x to obtain y =f(x) and then applying g to the result y to obtain g(y) = g(f(x)). In the notation the function that is applied first is always written on the right.
The composition is an operation on functions that is defined only if the codomain of the first function is the domain of the second one. Even when and are both defined, the composition is not commutative. For example, if f(x) = x2 and g(x) = x + 1, one has
The function composition is associative in the sense that, if one of and is defined, then the other is also defined, and they are equal. Thus, one writes
The identity functions and are respectively a right identity and a left identity for functions from X to Y. That is, if f is a function with domain X, and codomain Y, one has
-
A composite function g(f(x)) can be visualized as the combination of two "machines".
-
A simple example of a function composition
-
Another composition. For example, we have here (g ∘ f )(c) = #.
Image and preimage
Let The image by f of an element x of the domain X is f(x). If A is any subset of X, then the image of A by f, denoted f(A) is the subset of the codomain Y consisting of all images of elements of A, that is,
The image of f is the image of the whole domain, that is f(X). It is also called the range of f, although the term may also refer to the codomain.[5]
On the other hand, the inverse image, or preimage by f of a subset B of the codomain Y is the subset of the domain X consisting of all elements of X whose images belong to B. It is denoted by That is
For example, the preimage of {4, 9} under the square function is the set {−3,−2,2,3}.
By definition of a function, the image of an element x of the domain is always a single element of the codomain. However, the preimage of a single element y, denoted may be empty or contain any number of elements. For example, if f is the function from the integers to themselves that map every integer to 0, then f−1(0) = Z.
If is a function, A and B are subsets of X, and C and D are subsets of Y, then one has the following properties:
The preimage by f of an element y of the codomain is sometimes called, in some contexts, the fiber of y under f.
If a function f has an inverse (see below), this inverse is denoted In this case may denote either the image by or the preimage by f of C. This is not a problem, as these sets are equal. The notation and may be ambiguous in the case of sets that contain some subsets as elements, such as In this case, some care may be needed, for example, by using square brackets for images and preimages of subsets, and ordinary parentheses for images and preimages of elements.
Injective, surjective and bijective functions
Let be a function.
The function f is injective (or one-to-one, or is an injection) if f(a) ≠ f(b) for any two different elements a and b of X. Equivalently, f is injective if, for any the preimage contains at most one element. An empty function is always injective. If X is not the empty set, and if, as usual, the axiom of choice is assumed, then f is injective if and only if there exists a function such that that is, if f has a left inverse. The axiom of choice is needed, because, if f is injective, one defines g by if and by , if where is an arbitrarily chosen element of X.
The function f is surjective (or onto, or is a surjection) if the range is equals the codomain, that is, if f(X) = Y. In other words, the preimage of every is nonempty. If, as usual, the axiom of choice is assumed, then f is surjective if and only if there exists a function such that that is, if f has a right inverse. The axiom of choice is needed, because, if f is injective, one defines g by where is an arbitrarily chosen element of
The function f is bijective (or is bijection or a one-to-one correspondence) if it is both injective and surjective. That is f is bijective if, for any the preimage contains exactly one element. The function f is bijective if and only if it admits an inverse function, that is a function such that and (Contrarily to the case of injections and surjections, this does not require the axiom of choice.)
Every function may be factorized as the composition i ∘ s of a surjection followed by an injection, where s is the canonical surjection of X onto f(X), and i is the canonical injection of f(X) into Y. This is the canonical factorization of f.
"One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the Bourbaki group and imported into English. As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "f maps X onto Y" differs from "f maps X into B" in that the former implies that f is surjective), while the latter makes no assertion about the nature of f the mapping. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage to be more symmetrical.
Restriction and extension
If is a function, and S is a subset of X, then the restriction of f to S, denoted f|S, is the function from S to Y that is defined by
This often used for define partial inverse functions: if there is a subset S of a function f such that f|S is injective, then the canonical surjection of f|S on its image f|S(S) = f(S) is a bijection, which has an inverse function from f(S) to S. This is in this way that inverse trigonometric functions are defined. The cosine function, for example, is injective, when restricted to the interval (–0, π); the image of this restriction is the interval (–1, 1); this defines thus an inverse function from (–1, 1) to (–0, π), which is called arccosine and denoted arccos.
Function restriction may also be used for "gluing" functions together: let be the decomposition of X as a union of subsets. Suppose that a function is defined on each such that, for each pair of indices, the restrictions of and to are equal. Then, this defines a unique function such that for every i. This is generally in this way that functions on manifolds are defined.
An extension of a function f is a function g such that f is a restriction of g. A typical use of this concept is the process of analytic continuation, that allows extending functions whose domain is a small part of the complex plane to functions whose domain is almost the whole complex plane.
Here is another classical example of a function extension that is encountered when studying homographies of the real line. An homography is a function such that ad – bc ≠ 0. Its domain is the set of all real numbers different from and its image is the set of all real numbers different from If one extends the real line to the projectively extended real line by adding ∞ to the real numbers, one may extend h for being a bijection of the extended real line to itself, by setting and
Multivariate function

A multivariate function, or function of several variables is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time and its speed.
More formally, a function of n variables is a function whose domain is a set of n-tuples. For example, multiplication of integers is a function of two variables, or bivariate function, whose domain it the set of all pairs (2-uples) of integers and the codomain is the set of integers. The same is true for every binary operation. More generally, every mathematical operation is defined as a multivariate function.
The direct product of n sets is the set of all n-uples such that for every i. Therefore, a function of n variables is a function
where the domain U has the form
When using the functional notation, one omits the parentheses surrounding tuples. That is, one write , and not
In the case where all s are equal to the set of real numbers, one has a function of several real variables. If the s are equal to the set of complex numbers, one has a function of several complex variables
It is common to consider also functions whose codomain is a product of sets. For example, Euclidean division maps very pair (a, b) of integers with b ≠ 0 to a pair of integers called the quotient and the remainder.
The codomain may also be a vector space. In this case, one talks of a vector-valued function. If the domain is contained in a Euclidean space, or more generally a manifold, a vector-valued function is often called a vector field.
In calculus
The idea of function, starting in the 17th century, was fundamental to the new infinitesimal calculus (see History of the function concept). At that time, only real-valued functions of a real variable were considered, and all functions were assumed to be smooth. But the definition was soon extended to functions of several variables and to function of a complex variable. In the second half of 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined.
Functions are now used throughout all areas of mathematics. In introductory calculus, when the word function is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as real analysis and complex analysis.
Real function


A real function is a real-valued function of a real variable, that is, a function whose codomain is the field of real numbers and whose domain is a set of real numbers that contains an interval. In this section, these functions are simply called functions.
The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are continuous, differentiable, and even analytic. This regularity insures that these functions can be visualized by their graphs. In this section, all functions are differentiable in some interval.
Functions enjoy pointwise operations, that is, if f and g are functions, their sum, difference and product are functions defined by
The domains of the resulting functions are the intersection of the domains of f and g. The quotient of two functions is defined similarly by
but the domain of the resulting function is obtained by removing the zeros of g from the intersection of the domains of f and g.
The polynomial functions are defined by polynomials, and their domain is the whole set of real numbers. They include constant functions, linear functions and quadratic functions. Rational functions are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid division by zero. The simplest rational function is the function whose graph is an hyperbola, and whose domain is the whole real line except for 0.
The derivative of a real differentiable function is a real function. An antiderivative of a continuous real function is a real function that is differentiable in any open interval in which the original function is continuous. For example, the function is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for x = 1, is a differentiable function called the natural logarithm.
A real function f is monotonic in an interval if the sign of does not depend of the choice of x and y in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function f is monotonic in an interval I, it has an inverse function, which is a real function with domain f(I) and image I. This is how inverse trigonometric functions are defined in terms of trigonometric functions, where the trigonometric functions are monotonic. Another example: the natural logarithm is monotonic on the positive real numbers, and its image is the whole real line; therefore it has an inverse function that is a bijection between the real numbers and the positive real numbers. This inverse is the exponential function.
Many other real functions are defined either by the implicit function theorem (the inverse function is a particular instance) or as solutions of differential equations. For example the sine and the cosine functions are the solutions of the linear differential equation
such that
Complex function
Function of several real or complex variables
Vector-valued function
Function space
In mathematical analysis, and more specifically in functional analysis, a function space is a set of scalar-valued or vector-valued functions, which share a specific property and form a topological vector space. For example, the real smooth functions with a compact support (that is, they are zero outside some compact set) form a function space that is at the basis of the theory of distributions.
Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and topological properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ordinary or partial differential equations result of the study of function spaces.
Multi-valued functions

Several methods for specifying functions of real or complex variables start from a local definition of the funcion at a point or on a neighbourhood of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point there are several possible starting values for the function.
For example, for defining the square root function as the inverse function of the square function, one may choose any positive real number for and there are two choices for the value of the function, one which is positive and denoted and the other that is denoted These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one see that, together, they form a single smooth curve. It is therefore often useful to consider these two square root functions as a single function that has two values for positive x, one value for 0 and no value for negative x.
In the preceding example, one choice, the positive square root, is more natural then the other. This is not the case in general. For example, let consider the implicit function that maps y to a root x of (see the figure on the right). For y = 0 one may choose either for x. By the implicit function theorem, each choice defines a function; for the first one, the (maximal) domain is the interval [–2, 2] and the image is [–1, 1]; for the second one, the domain is [–2, +∞) and the image is [1, +∞); for the last one, the domain is (–∞, 2] and the image is (–∞, –1]. As the three graphs together form a smooth curve, and there is no reason for preferring one choice, these three functions are often considered as a single multi-valued function of y that has three values for –2 < y < 2, and only one value for y ≤ –2 and y ≥ –2.
Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically analytic functions. The domain to which a complex function is analytic may be extended by analytic continuation consists generally of almost the whole complex plane. However, it is frequent that, when extending the domain through two different paths, one gets different values. For example, when extending the domaine of the square root function, along a path of complex numbers with positive imaginary parts, one gets i for the square root of –1, while, when extending through complex numbers with negative imaginary parts, one gets –i. There are generally two ways for solving the problem. One may define a function that is not continuous along some curve, called branch cut. Such a function is called the principal value of the function. The other way is to consider that one has a multi-valued function, which is analytic everywhere except for isolated singularities, but whose value may "jump" if one follows a closed loop around a singularity. This jump is called the monodromy.
In foundations of mathematics and set theory
The definition of a function that is given in this article requires the concept of set, since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is general not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions.
For example the singleton set may be considered as a function Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definition for these weakly specified functions.[6]
These generalized functions may be critical in the development of a formalization of foundations of mathematics. For example, the Von Neumann–Bernays–Gödel set theory, is an extension of the set theory in which the collection of all sets is a class. This theory includes the replacement axiom, which may be interpreted as "if X is a set, and F is a function, then F[X] is a set".
In computer science
See also
Subpages
Generalizations
Related topics
Notes
- ^ The words map or mapping, transformation, correspondence, and operator are often used synonymously. Halmos 1970, p. 30.
- ^ MacLane, Saunders; Birkhoff, Garrett (1967). Algebra (First ed.). New York: Macmillan. pp. 1–13.
- ^ Spivak 2008, p. 39.
- ^ Hamilton, A. G. Numbers, sets, and axioms: the apparatus of mathematics. Cambridge University Press. p. 83. ISBN 0-521-24509-5.
- ^ Quantities and Units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology, page 15. ISO 80000-2 (ISO/IEC 2009-12-01)
- ^ Gödel 1940, p. 16; Jech 2003, p. 11; Cunningham 2016, p. 57
References
- Bartle, Robert (1967). The Elements of Real Analysis. John Wiley & Sons.
{{cite book}}: Invalid|ref=harv(help) - Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. ISBN 978-1-4419-7126-5.
{{cite book}}: Invalid|ref=harv(help) - Cunningham, Daniel W. (2016). Set theory: A First Course. Cambridge University Press. ISBN 978-1107120327.
{{cite book}}: Invalid|ref=harv(help) - Gödel, Kurt (1940). The Consistency of the Continuum Hypothesis. Princeton University Press. ISBN 978-0691079271.
{{cite book}}: Invalid|ref=harv(help) - Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 0-387-90092-6.
{{cite book}}: Invalid|ref=harv(help) - Jech, Thomas (2003). Set theory (Third Millennium ed.). Springer-Verlag. ISBN 3-540-44085-2.
{{cite book}}: Invalid|ref=harv(help) - Spivak, Michael (2008). Calculus (4th ed.). Publish or Perish. ISBN 978-0-914098-91-1.
{{cite book}}: Invalid|ref=harv(help)
Further reading
- Anton, Howard (1980). Calculus with Analytical Geometry. Wiley. ISBN 978-0-471-03248-9.
- Bartle, Robert G. (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05464-1.
- Dubinsky, Ed; Harel, Guershon (1992). The Concept of Function: Aspects of Epistemology and Pedagogy. Mathematical Association of America. ISBN 0-88385-081-8.
- Hammack, Richard (2009). "12. Functions" (PDF). Book of Proof. Virginia Commonwealth University. Retrieved 2012-08-01.
- Husch, Lawrence S. (2001). Visual Calculus. University of Tennessee. Retrieved 2007-09-27.
- Katz, Robert (1964). Axiomatic Analysis. D. C. Heath and Company.
- Kleiner, Israel (1989). Evolution of the Function Concept: A Brief Survey. Vol. 20. Mathematical Association of America. pp. 282–300. doi:10.2307/2686848. JSTOR 2686848.
{{cite book}}:|journal=ignored (help) - Lützen, Jesper (2003). "Between rigor and applications: Developments in the concept of function in mathematical analysis". In Porter, Roy (ed.). The Cambridge History of Science: The modern physical and mathematical sciences. Cambridge University Press. ISBN 0521571995. An approachable and diverting historical presentation.
- Malik, M. A. (1980). Historical and pedagogical aspects of the definition of function. Vol. 11. pp. 489–492. doi:10.1080/0020739800110404.
{{cite book}}:|journal=ignored (help) - Reichenbach, Hans (1947) Elements of Symbolic Logic, Dover Publishing Inc., New York NY, ISBN 0-486-24004-5.
- Ruthing, D. (1984). Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N. Vol. 6. pp. 72–77.
{{cite book}}:|journal=ignored (help) - Thomas, George B.; Finney, Ross L. (1995). Calculus and Analytic Geometry (9th ed.). Addison-Wesley. ISBN 978-0-201-53174-9.
External links
- "Function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Function". MathWorld.
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- NIST Digital Library of Mathematical Functions








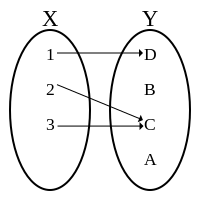














































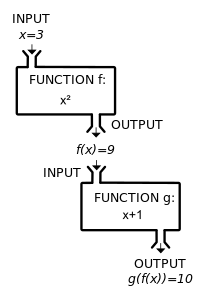


















![{\displaystyle f[A],f^{-1}[C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d728b72b3681c1a33529ac867bc49952dc812a4)




















































