| Snub order-6 square tiling | |
|---|---|
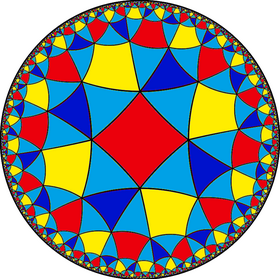 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 3.3.3.4.3.4 |
| Schläfli symbol | s(4,4,3) s{4,6} |
| Wythoff symbol | | 4 4 3 |
| Coxeter diagram |      
|
| Symmetry group | [(4,4,3)]+, (443) [6,4+], (4*3) |
| Dual | Order-4-4-3 snub dual tiling |
| Properties | Vertex-transitive |
In geometry, the snub order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of s{(4,4,3)} or s{4,6}.
Images[edit]
Symmetry[edit]
The symmetry is doubled as a snub order-6 square tiling, with only one color of square. It has Schläfli symbol of s{4,6}.
Related polyhedra and tiling[edit]
The vertex figure 3.3.3.4.3.4 does not uniquely generate a uniform hyperbolic tiling. Another with quadrilateral fundamental domain (3 2 2 2) and 2*32 symmetry is generated by 
:
| Uniform (4,4,3) tilings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,3)] (*443) | [(4,4,3)]+ (443) |
[(4,4,3+)] (3*22) |
[(4,1+,4,3)] (*3232) | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}1/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}1/2 t0,2(4,4,3) |
t{4,6}1/2 t0,1,2(4,4,3) |
s{4,6}1/2 s(4,4,3) |
hr{4,6}1/2 hr(4,3,4) |
h{4,6}1/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Uniform duals | ||||||||||
|
|
|
|
|||||||
| V(3.4)4 | V3.8.4.8 | V(4.4)3 | V3.8.4.8 | V(3.4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3)2 | V66 | V4.3.4.6.6 |
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
=    = = 
|
= 
|
= = =
|
=
|
= = = 
|
=
|
| |||||
|
|
|
|
|
|
| |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
=
|
= 
|
=  
|
=
|
= 
|
= 
|
| |||||
|
|
|
|
|
|
|
| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
See also[edit]
Footnotes[edit]
References[edit]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links[edit]
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
Well, that’s interesting to know that Psilotum nudum are known as whisk ferns. Psilotum nudum is the commoner species of the two. While the P. flaccidum is a rare species and is found in the tropical islands. Both the species are usually epiphytic in habit and grow upon tree ferns. These species may also be terrestrial and grow in humus or in the crevices of the rocks.
View the detailed Guide of Psilotum nudum: Detailed Study Of Psilotum Nudum (Whisk Fern), Classification, Anatomy, Reproduction