THC Science

Conical spiral with an archimedean spiral as floor projection

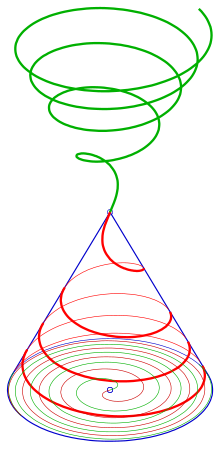
In mathematics, a conical spiral, also known as a conical helix,^[1] is a space curve on a right circular cone, whose floor projection is a plane spiral. If the floor projection is a logarithmic spiral, it is called conchospiral (from conch).

Parametric representation

In the $x$ - $y$ -plane a spiral with parametric representation

x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi

a third coordinate $z(\varphi )$ can be added such that the space curve lies on the cone with equation $\;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;$ :

$x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .$

Such curves are called conical spirals.^[2] They were known to Pappos.

Parameter $m$ is the slope of the cone's lines with respect to the $x$ - $y$ -plane.

A conical spiral can instead be seen as the orthogonal projection of the floor plan spiral onto the cone.

Examples

1) Starting with an archimedean spiral

\;r(\varphi )=a\varphi \;

gives the conical spiral (see diagram)

x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .

In this case the conical spiral can be seen as the intersection curve of the cone with a helicoid.

2) The second diagram shows a conical spiral with a Fermat's spiral

\;r(\varphi )=\pm a{\sqrt {\varphi }}\;

as floor plan.

3) The third example has a logarithmic spiral

\;r(\varphi )=ae^{k\varphi }\;

as floor plan. Its special feature is its constant slope (see below).

Introducing the abbreviation

K=e^{k}

gives the description:

r(\varphi )=aK^{\varphi }

.

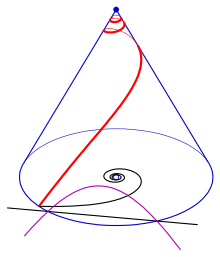
4) Example 4 is based on a hyperbolic spiral

\;r(\varphi )=a/\varphi \;

. Such a spiral has an asymptote (black line), which is the floor plan of a hyperbola (purple). The conical spiral approaches the hyperbola for

\varphi \to 0

.

Properties

The following investigation deals with conical spirals of the form $r=a\varphi ^{n}$ and $r=ae^{k\varphi }$ , respectively.

Slope

The slope at a point of a conical spiral is the slope of this point's tangent with respect to the $x$ - $y$ -plane. The corresponding angle is its slope angle (see diagram):

\tan \beta ={\frac {z'}{\sqrt {(x')^{2}+(y')^{2}}}}={\frac {mr'}{\sqrt {(r')^{2}+r^{2}}}}\ .

A spiral with $r=a\varphi ^{n}$ gives:

$\tan \beta ={\frac {mn}{\sqrt {n^{2}+\varphi ^{2}}}}\ .$

For an archimedean spiral is $n=1$ and hence its slope is $\ \tan \beta ={\tfrac {m}{\sqrt {1+\varphi ^{2}}}}\ .$

For a logarithmic spiral with $r=ae^{k\varphi }$ the slope is $\ \tan \beta ={\tfrac {mk}{\sqrt {1+k^{2}}}}\$ ( $\color {red}{\text{ constant!}}$ ).

Because of this property a conchospiral is called an equiangular conical spiral.

Arclength

The length of an arc of a conical spiral can be determined by

L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(x')^{2}+(y')^{2}+(z')^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2})(r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .

For an archimedean spiral the integral can be solved with help of a table of integrals, analogously to the planar case:

L={\frac {a}{2}}\left[\varphi {\sqrt {(1+m^{2})+\varphi ^{2}}}+(1+m^{2})\ln \left(\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}\right)\right]_{\varphi _{1}}^{\varphi _{2}}\ .

For a logarithmic spiral the integral can be solved easily:

L={\frac {\sqrt {(1+m^{2})k^{2}+1}}{k}}(r{\big (}\varphi _{2})-r(\varphi _{1}){\big )}\ .

In other cases elliptical integrals occur.

Development

For the development of a conical spiral^[3] the distance $\rho (\varphi )$ of a curve point $(x,y,z)$ to the cone's apex $(0,0,z_{0})$ and the relation between the angle $\varphi$ and the corresponding angle $\psi$ of the development have to be determined:

\rho ={\sqrt {x^{2}+y^{2}+(z-z_{0})^{2}}}={\sqrt {1+m^{2}}}\;r\ ,

\varphi ={\sqrt {1+m^{2}}}\psi \ .

Hence the polar representation of the developed conical spiral is:

$\rho (\psi )={\sqrt {1+m^{2}}}\;r({\sqrt {1+m^{2}}}\psi )$

In case of $r=a\varphi ^{n}$ the polar representation of the developed curve is

\rho =a{\sqrt {1+m^{2}}}^{\,n+1}\psi ^{n},

which describes a spiral of the same type.

If the floor plan of a conical spiral is an archimedean spiral than its development is an archimedean spiral.

In case of a hyperbolic spiral (

n=-1

) the development is congruent to the floor plan spiral.

In case of a logarithmic spiral $r=ae^{k\varphi }$ the development is a logarithmic spiral:

\rho =a{\sqrt {1+m^{2}}}\;e^{k{\sqrt {1+m^{2}}}\psi }\ .

Tangent trace

The trace (purple) of the tangents of a conical spiral with a hyperbolic spiral as floor plan. The black line is the asymptote of the hyperbolic spiral.

The collection of intersection points of the tangents of a conical spiral with the $x$ - $y$ -plane (plane through the cone's apex) is called its tangent trace.

For the conical spiral

(r\cos \varphi ,r\sin \varphi ,mr)

the tangent vector is

(r'\cos \varphi -r\sin \varphi ,r'\sin \varphi +r\cos \varphi ,mr')^{T}

and the tangent:

x(t)=r\cos \varphi +t(r'\cos \varphi -r\sin \varphi )\ ,

y(t)=r\sin \varphi +t(r'\sin \varphi +r\cos \varphi )\ ,

z(t)=mr+tmr'\ .

The intersection point with the $x$ - $y$ -plane has parameter $t=-r/r'$ and the intersection point is

$\left({\frac {r^{2}}{r'}}\sin \varphi ,-{\frac {r^{2}}{r'}}\cos \varphi ,0\right)\ .$

$r=a\varphi ^{n}$ gives $\ {\tfrac {r^{2}}{r'}}={\tfrac {a}{n}}\varphi ^{n+1}\$ and the tangent trace is a spiral. In the case $n=-1$ (hyperbolic spiral) the tangent trace degenerates to a circle with radius $a$ (see diagram). For $r=ae^{k\varphi }$ one has $\ {\tfrac {r^{2}}{r'}}={\tfrac {r}{k}}\$ and the tangent trace is a logarithmic spiral, which is congruent to the floor plan, because of the self-similarity of a logarithmic spiral.

References

^ "Conical helix". MATHCURVE.COM. Retrieved 2022-03-03.
^ Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: Geschichte der mathematik. G. J. Göschen, 1921, p. 92.
^ Theodor Schmid: Darstellende Geometrie. Band 2, Vereinigung wissenschaftlichen Verleger, 1921, p. 229.

External links

Jamnitzer-Galerie: 3D-Spiralen. Archived 2021-07-02 at the Wayback Machine.
Weisstein, Eric W. "Conical Spiral". MathWorld.

[MATHCURVE.COM-1] "Conical helix". MATHCURVE.COM. Retrieved 2022-03-03.

[2] Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: Geschichte der mathematik. G. J. Göschen, 1921, p. 92.

[3] Theodor Schmid: Darstellende Geometrie. Band 2, Vereinigung wissenschaftlichen Verleger, 1921, p. 229.

[1]

[2]

[3]